As operações com Conjuntos
Quais são as operações com conjuntos?

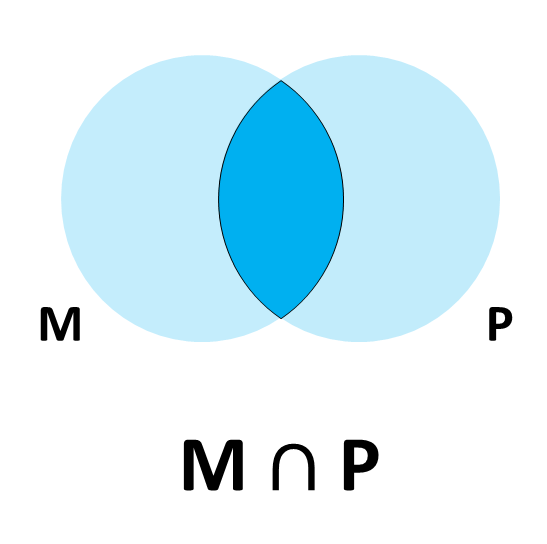
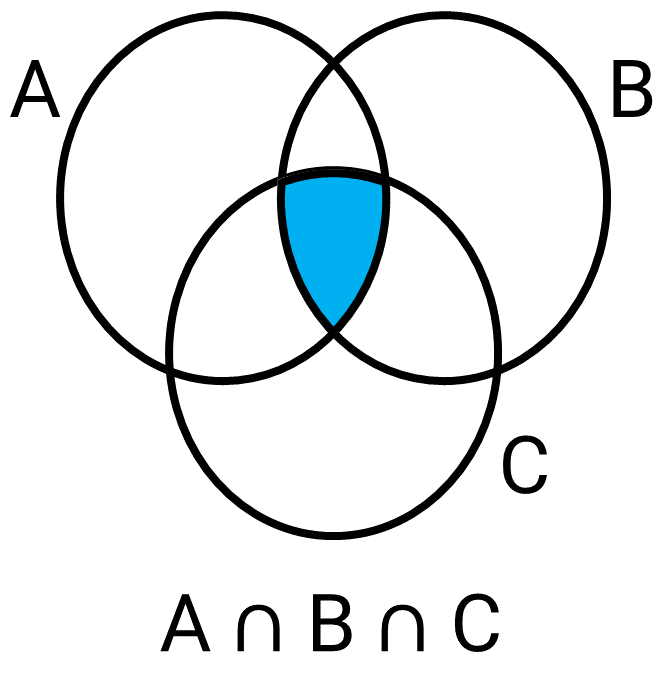
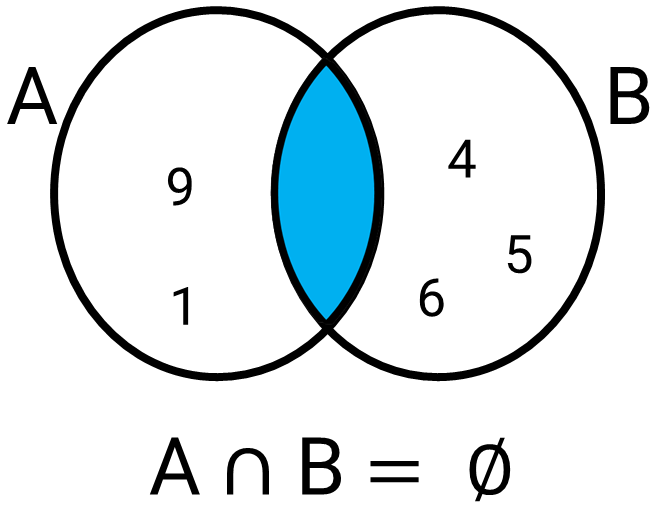

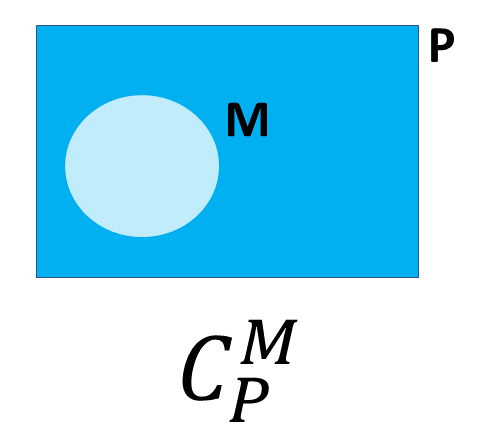
Subconjuntos e conjunto das partes

Que tal praticar um pouco?
"Não existe transformação sem aprendizado e conhecimento."
Aristóteles
1) Dados os conjuntos [math] A \ \cup \ B = \{ 4, 3, 2, 1 \} [/math]; [math] A - B = \{ 2, 3 \} [/math] e [math] A \ \cap \ B = \{ 1 \} [/math]. Pode-se afirmar que conjunto [math] B [/math] é formado por:
2) Sendo [math] R = \{ 10,11, 12, 13, 14 \} [/math] e [math] S = \{ 12, 13, 14 \} [/math]; o complementar de [math] S [/math] em [math] R [/math] será o conjunto:
3) Seja [math] P [/math] o conjunto das partes de um conjunto [math] B [/math] formado pelos seguintes elementos: [math] [\emptyset, \{ 1 \}, \{ 2 \}, \{ 1,2 \}] [/math]. Nesse caso, podemos afirmar que o conjunto [math] B [/math] será igual a:
4) Sabendo que um determinado conjunto [math] R [/math] possui [math] 5 [/math] elementos, a quantidade de subconjuntos necessários para formar o conjunto das partes deste conjunto [math] R [/math] será exatamente igual a:
5) Seja [math] A = \{ 31, 32, 33, 34, 35 \} [/math]; [math] B = \{ 34, 35, 36, 37 \} [/math] e [math] C = \{ 32, 33, 34 \} [/math]. O conjunto [math] A \ \cap \ B \ \cap \ C [/math] será?
Temas relacionados:
Conjuntos
Relações com Conjuntos
Subconjuntos
Algarismos romanos
Operações com algarismos romanos
Operações com algarismos romanos - multiplicação
Sistema de numeração decimal
Números naturais
Adição de números naturais
Propriedades da adição
Subtração de números naturais
Multiplicação de números naturais
Propriedades da multiplicação
Divisão de números naturais
Potenciação de números naturais
Radiciação de números naturais
Conjunto dos números naturais - parte 2

