A multiplicação de algarismos romanos
Vamos falar agora de forma bem particular, da multiplicação de algarismos romanos. Fique bem atento a esta aula e não perca nenhum detalhe.

Os irmãos Letícia, Leonardo e Lídia estavam passando alguns dias em Roma. No roteiro que programaram estava a visita a diversas ruínas famosas do antigo império. Como de costume Leticia resolver desafiar os irmãos:
"Qual de vocês conseguiria me mostrar o resultado do produto de 145 por 26 passo a passo utilizando apenas algarismos romanos?"
"Você quer dizer multiplicar esses dois números utilizando algarismos romanos sem usar a conversão para o sistema decimal Leticia?" Respondeu Lídia.
"Exatamente! E ai? Algum de vocês dois conseguiria tal façanha?" Questionou mais uma vez Leticia empolgada.
" Sei como realizar tais cálculos maninha!" Exclamou Leonardo. "E vamos fazer isso agora mesmo! Meninas, caneta e papel na mão!" Concluiu.
Então Leonardo inicia sua explicação.
"Lembram do exemplo que utilizamos uma vez quando calculamos na escola uma multiplicação de algarismos romanos solicitada pelo professor? Pois bem, primeiro vou recordar com vocês como efetuamos um produto utilizando o atual sistema decimal de numeração. Vamos recordar."
Vou efetuar a seguinte multiplicação abaixo.

"Bem simples correto! Foi utilizada a conversão de romanos para decimais, efetuados os cálculo e depois realizada a conversão de novo." Explica Leonardo.
E continua. "Só que mais uma vez, vamos ver como seriam efetuados esses cálculos sem essa conversão."
Multiplicação de algarismos romanos sem a conversão em decimais
"Para efetuarmos a multiplicação de algarismos romanos sem a conversão para decimais precisamos ter a atenção redobrada mas não é uma tarefa complicada."
"Você vai precisar ter conhecimento da propriedade distributiva da multiplicação e de uma tabuada própria composta somente de algarismos romanos."
"A tabuada utilizada será a demonstrada abaixo veja:"
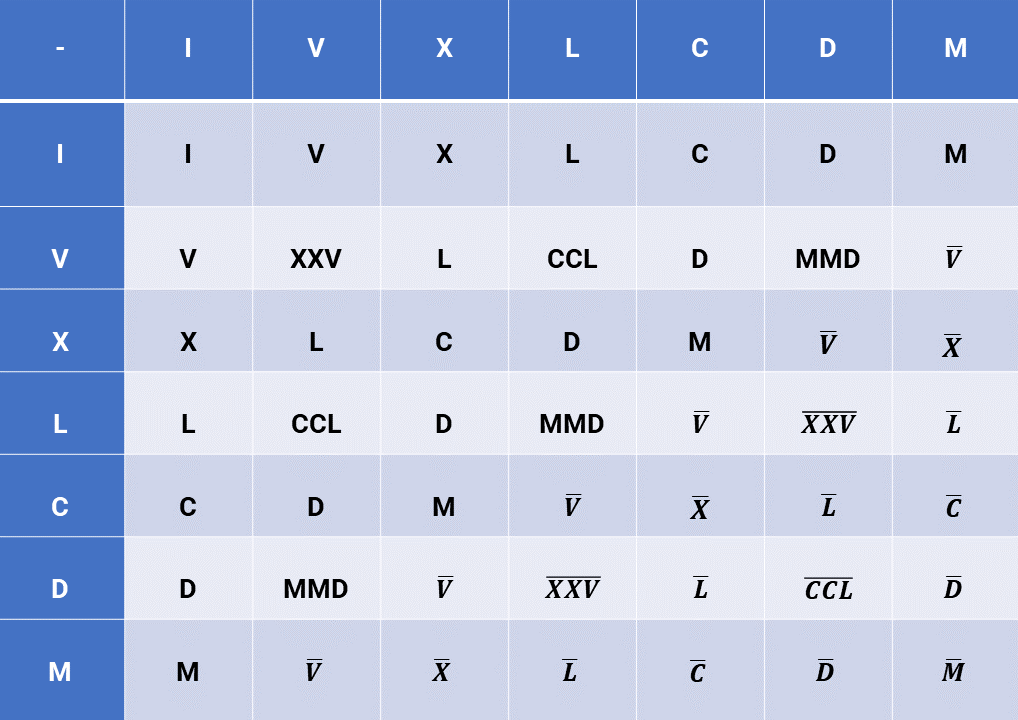
"A multiplicação de algarismos romanos é feito nesta tabuada da mesma forma que a tabuada de números naturais. Multiplicamos um item da linha por um item da coluna."
"Por exemplo a multiplicação de [math] X [/math] vezes [math] X [/math] resulta em [math] C [/math]. Em decimais temos o equivalente: [math] 10 [/math] vezes [math] 10 [/math] igual a [math] 100 [/math]."
"Vamos multiplicar então:"
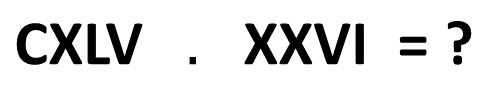
Neste momento utilizamos o ponto para representar o operador da multiplicação. Isto é feito para não haver confusão com a letra [math] X [/math] que representa [math] 10 [/math] em romanos.
Começamos mais uma vez com os mesmos desmontes aplicados na adição e subtração.

Aqui a única subtração alterada foi [math] XL [/math] que passou a ser igual a [math] XXXX [/math]. Veja como ficou depois e o destaque desta alteração em em vermelho.
Agora vamos armar esse cálculo. Utilizamos nesta etapa o símbolo comum do operador [math] (\times) [/math].
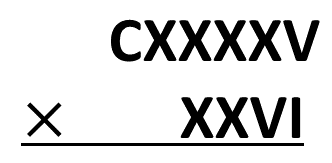
A multiplicação é feita como se estivéssemos resolvendo com números naturais. Primeiro multiplicamos o algarismo [math] I [/math] do multiplicador com cada um dos algarismos do multiplicando.
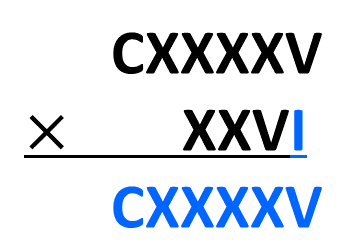
Assim tivemos o nosso primeiro resultado. Vamos agora multiplicar o próximo algarismo do multiplicador, no caso o [math] V [/math].
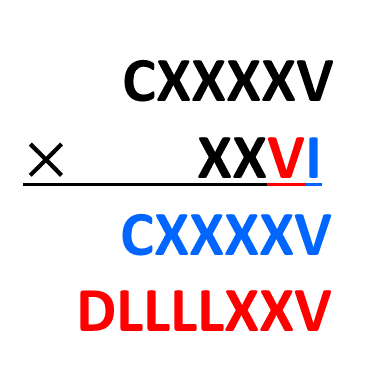
O que há de diferente aqui? Os algarismos ficam exatamente um embaixo do outro no resultado.
Não temos aquele espaço ou um zero como fazemos com os decimais.
O próximo passo é multiplicar agora o primeiro [math] X [/math] por cada algarismo do multiplicando.
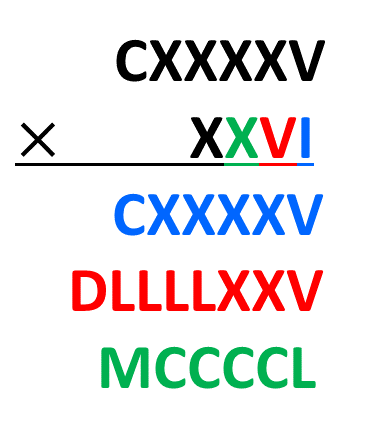
Por fim multiplicamos o algarismo [math] X [/math] que restou.
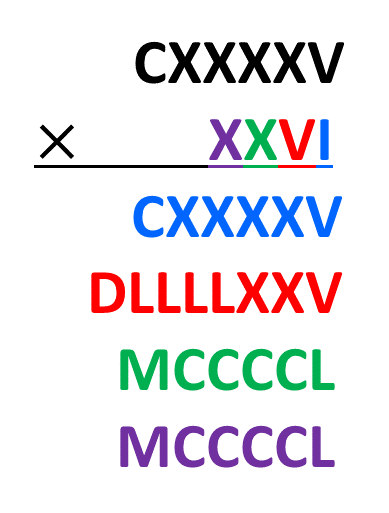
Agora basta efetuar a soma como já foi mencionado anteriormente. Aqui não temos subtrações a serem "desmontadas".
Então basta agrupar os algarismos e ir calculando. Faremos juntos passo a passo novamente para você não ter mais dúvidas sobre a adição.

Como não há subtrações, agrupamos os algarismos idênticos e vamos somando. Sempre que possível convertemos, iniciando com os de menor valor para os de maior valor.
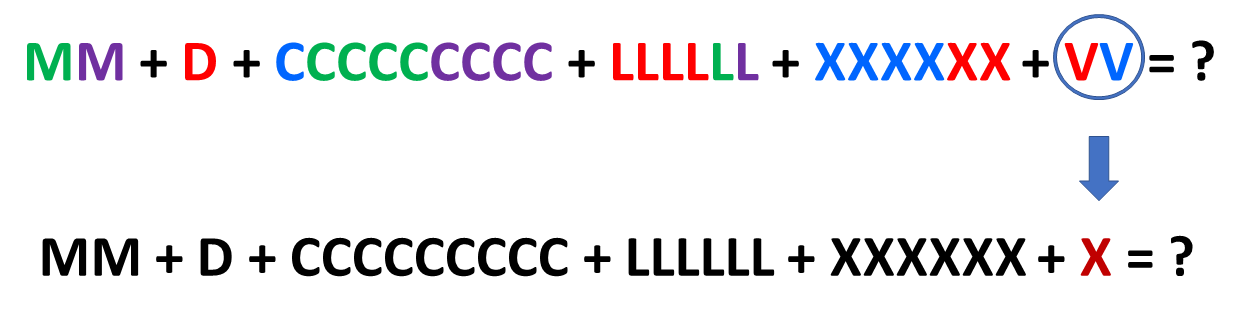
Seguimos juntando e convertendo.
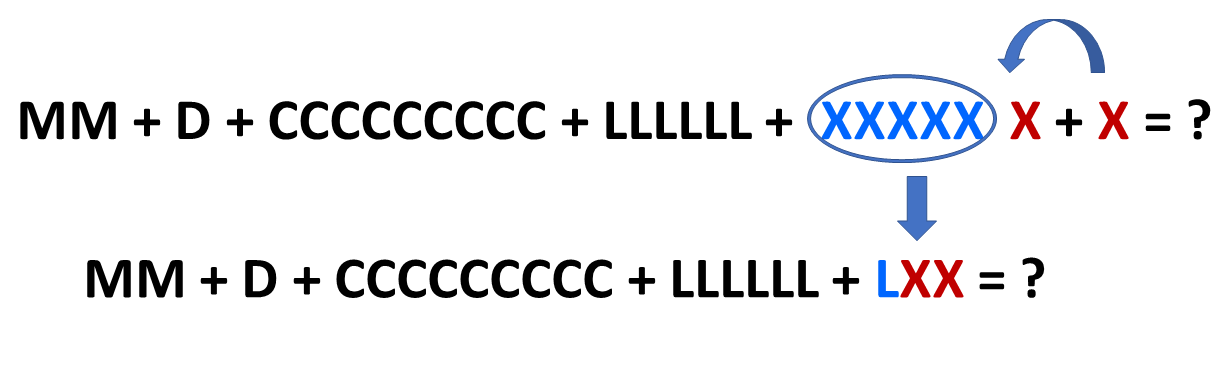
E continuamos os processos. Sempre focando em juntar algarismos iguais para possíveis conversões.
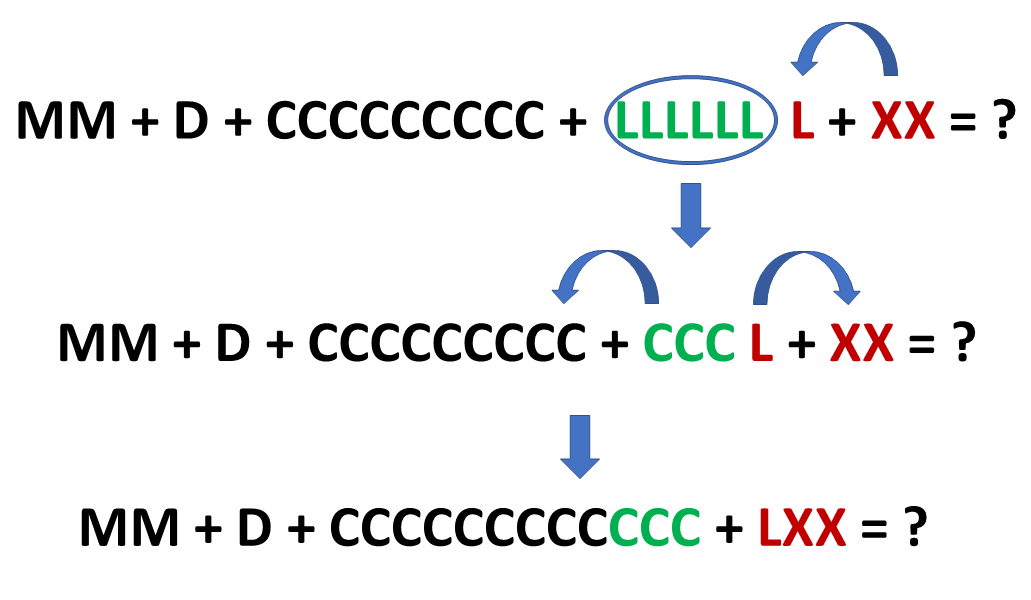
Pode parecer um pouco trabalhoso mas depois que você entende o padrão de cálculo tudo fica muito simples.
Observe como os algarismos vão diminuindo após cada conversão.
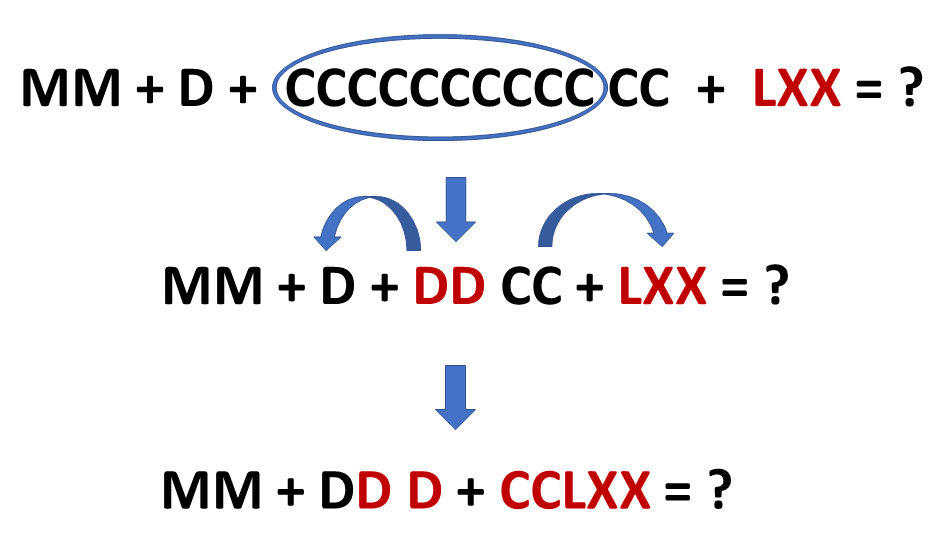
Nesta última imagem os valores de [math] C [/math] poderiam ser convertidos para [math] M [/math] tranquilamente já que [math] 10 C = 1 M [/math].
Preferi manter a conversão de [math] C [/math] para [math] D [/math] só para garantir o passo a passo. Finalmente estamos chegando ao final da operação. Ufa!
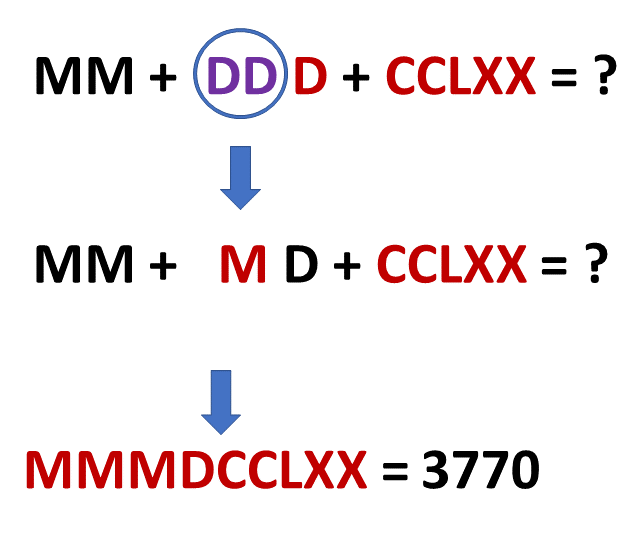
Pode conferir! Multiplicando [math] 145 [/math] por [math] 26 [/math] obtemos [math] 3770 [/math]. Hoje em dia não precisamos de todo esse trabalho devido a conversão em decimais.
Aqui simulamos como eram feitos os cálculos sem eles. No caso o mais importante aqui é o aprendizado do processo.
Que tal praticar um pouco?
"A verdade não resulta do número dos que nela creem."
Galileu Galilei
Efetue sem realizar a conversão em decimais:
1) Se efetuarmos o produto dos números [math] XLIV [/math] com o número [math] IX [/math] teremos como resultado em algarismos romanos o número?
Temas relacionados:
Conjuntos
Relações com conjuntos
Operações com Conjuntos
Subconjuntos
Algarismos romanos
Operações com algarismos romanos
Sistema de numeração decimal
Números naturais
Adição de números naturais
Propriedades da adição
Subtração de números naturais
Multiplicação de números naturais
Propriedades da multiplicação
Divisão de números naturais
Potenciação de números naturais
Radiciação de números naturais
Conjunto dos números naturais - parte 2

