As expressões algébricas
Manipular as expressões algébricas é um item fundamental para dominar a álgebra e resolver diversos problemas. Então vamos lá? Preparado?
Por que expressões algébricas?
Para que seus estudos sejam satisfatórios em álgebra, será necessário entender o que são as expressões algébricas.
Garanto a você que este assunto será bem tranquilo. Ao terminar este tópico você vai passar a entender como funciona uma área muito importante da matemática.
Bem, e o que vem a ser essa tal de expressão algébrica?
Toda expressão matemática composta por letras e números receberá este nome. Todas as letras presentes serão chamadas de variáveis ou incógnitas.
Os números que acompanham as letras são chamados coeficientes e os que estão acima das letras são chamados expoentes.
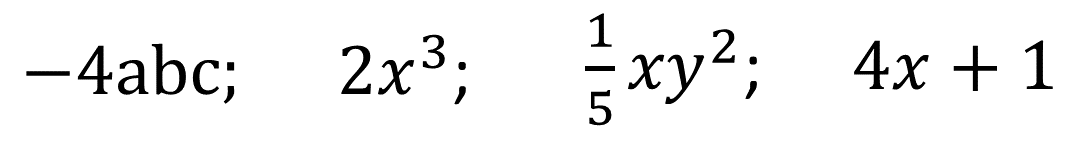
Termos de uma expressão algébrica
Essa união de letras e números determina o que chamamos de termo de uma expressão algébrica.
Pode haver apenas um ou vários deles na expressão.
Do mesmo modo que ocorreu com as expressões numéricas, os operadores matemáticos [math] (+, -, \times, \div) [/math] determinam a quantidade de termos existentes em uma expressão algébrica.
Atenção pois os operadores também pertencem ao termo.
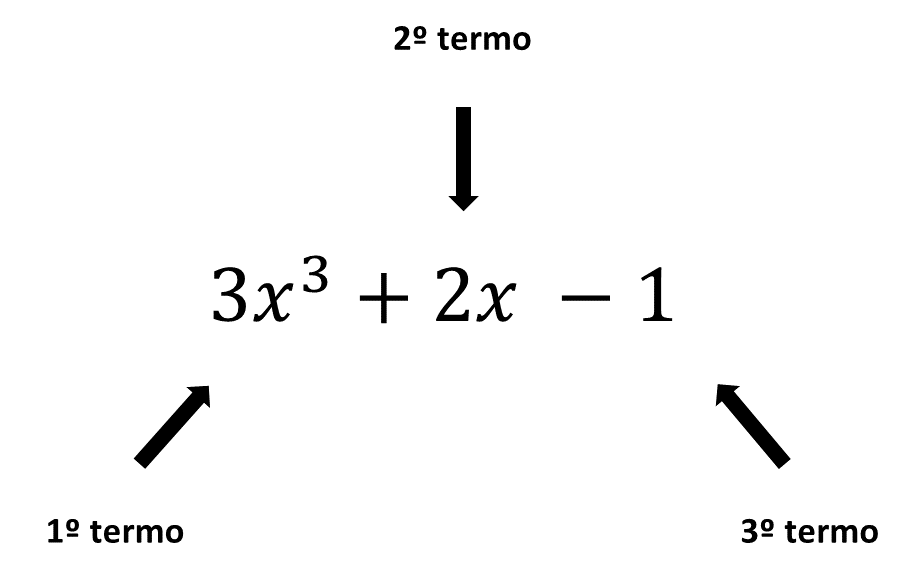
Na expressão algébrica acima temos [math] 3x ^{3} [/math] como um termo, [math] + \ 2x [/math] como outro termo e [math] – \ 1 [/math] como o último termo.
A parte numérica que multiplica as letras será chamada de coeficiente. Atenção pois, ele sempre será único em um termo.
Já o conjunto de todas as variáveis, incluindo seus expoentes, será chamado de parte literal.
Quando o expoente não tiver explícito, terá o valor um [math] ( 1 ) [/math] como já explicado em potenciação de números naturais.
Logo abaixo temos dois termos exemplificando a separação de cada um deles em coeficiente e parte literal. Veja:
termo: [math] 3 [/math] [math] x ^{3} [/math]
coeficiente [math] \rightarrow {3} [/math]
parte literal [math] \rightarrow x ^{3} [/math]
termo: [math] -15 [/math] [math] xy^ {2} z^ {3} [/math]
coeficiente [math] \rightarrow {- 15} [/math]
parte literal [math] \rightarrow {xy^ {2} z^ {3}} [/math]
Pode ocorrer de um termo não possuir nenhuma variável. Nesse caso, esse termo será chamado termo independente ou constante.
Valor numérico de uma expressão algébrica
Quando o valor de todas as variáveis em uma expressão algébrica for informado, será possível calcular o seu valor numérico.
Nesse caso, basta substituir o valor da incógnita pelo valor informado e pronto.
A expressão algébrica torna-se uma expressão numérica e seu cálculo será realizado de acordo com as regras já ensinadas.
Se você ainda tem alguma dúvida sobre expressões numéricas, recomendo dar uma olhadinha nesse assunto.
Vamos a um exemplo prático para que fique mais claro. Vamos encontrar o valor numérico para a seguinte expressão:
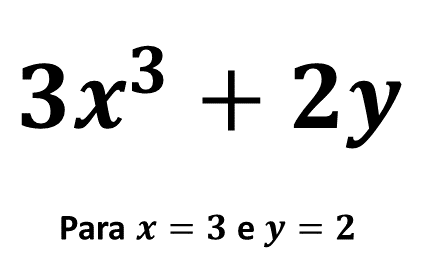
Observe que foi informado o valor que cada variável possui no momento do cálculo.
Agora o próximo passo é colocar esses valores nos seus devidos lugares. Vamos ao passo a passo.
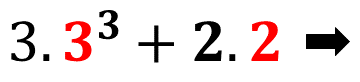
Veja que foram destacados em vermelho os números que substituíram as letras.
Todos na mesma ordem e no mesmo lugar. O próximo passo agora é calcular a potência.
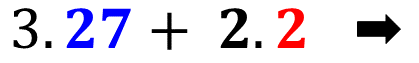
Então como aprendemos em expressões numéricas, agora é a vez da multiplicação e depois a soma.
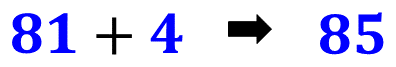
Concluindo, encontramos o valor [math] 85 [/math]. Podemos fazer cálculos com novas expressões ou com essa mesma utilizando valores diferentes para [math] x [/math] e [math] y [/math]. As possibilidades são infinitas.
Lembre-se apenas de respeitar as regras de operações de acordo com o conjunto numérico em questão.
Ou seja, se as expressões tiverem sinais, frações, potencias, raízes, etc.
Todas as regras que envolvem cálculos com esses itens devem ser rigorosamente respeitadas.
Termos semelhantes
Quando os termos possuírem a parte literal totalmente idêntica serão chamados de termos semelhantes.
Temos alguns exemplos na imagem abaixo. Observe os detalhes. Veja que os coeficientes diferem mas a parte literal é idêntica em todos os detalhes.

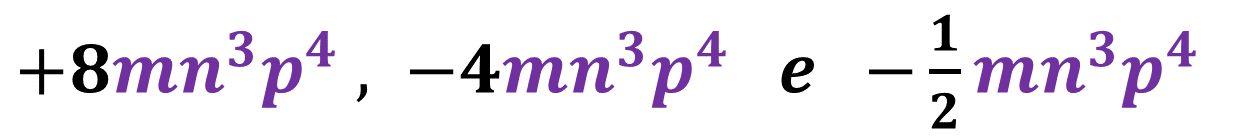
Exemplos de termos semelhantes
Adição e subtração de termos semelhantes
Termos semelhantes podem ser adicionados ou subtraídos. Dessa forma podemos reduzir expressões algébricas em expressões menores.
Para realizar uma dessas operações você deve conferir se realmente possuem a parte literal idêntica.
Depois reescreva a parte literal e calcule somente os coeficientes. Vamos para mais um exemplo para ficar mais evidente.
Vamos somar a expressão:
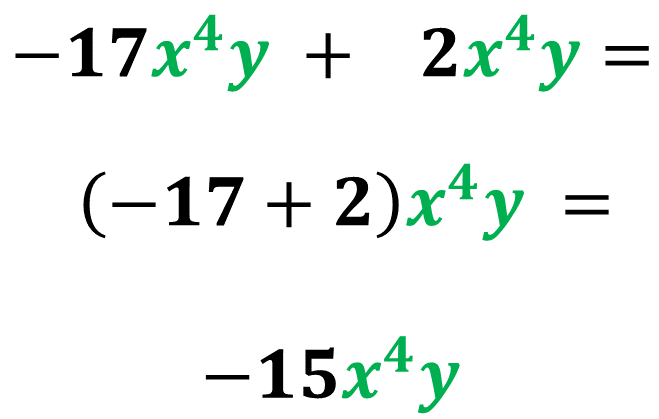
Como foi mencionado, o cálculo é feito apenas com os coeficientes. Da mesma forma assim seria feito a subtração, veja:
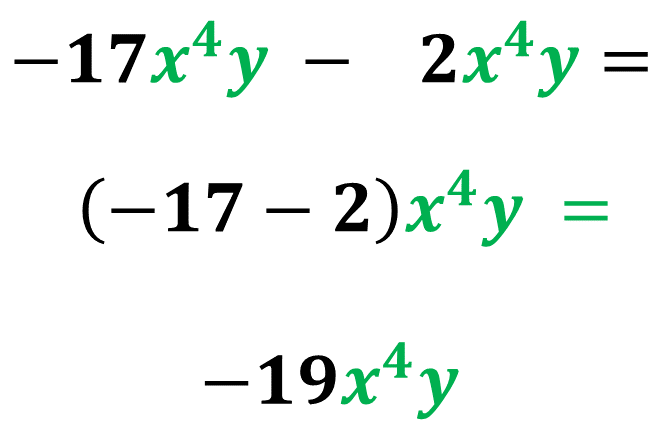
Multiplicação de termos algébricos
A multiplicação com termos semelhantes também poderá ser realizada.
Para este cálculo com as expressões algébricas você deverá estar atento as regras de potenciação.
Se você ainda não estudou este tópico ou tem dúvidas recomendo dar uma olhada.
Na prática a multiplicação aqui ocorre da seguinte forma: multiplique os coeficientes respeitando as regras de acordo com o tipo de número e para a parte literal, aplique as propriedades da potenciação variável a variável.
Como sempre faremos exemplos para ficar mais claro.
Vamos lá! Seja o produto:
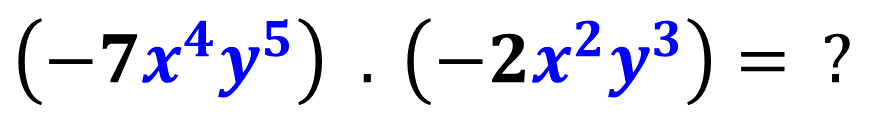
Qual será seu resultado? Bem, como foi falado, multiplicamos os coeficientes normalmente.
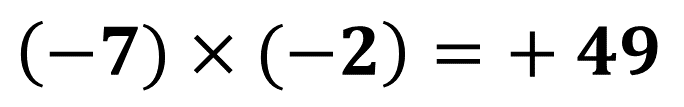
Depois aplicando as propriedades da potenciação para a parte literal obtemos.
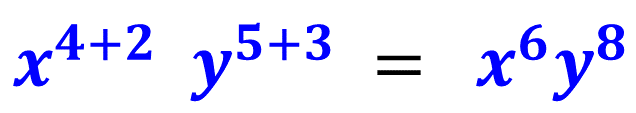
Nosso resultado final então ficou assim:
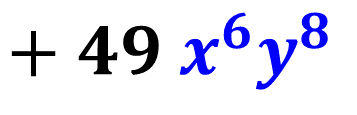
Equivalência em expressões algébricas
Expressões algébricas são classificadas como equivalentes quando, ao substituir suas variáveis por um valor numérico, resultam no mesmo valor.
Novamente vamos a um exemplo bem simples. Vamos verificar se as expressões
[math] 4k - 8 [/math] e [math] - 3k + 6 [/math]
são equivalentes para [math] k = + \ 2 [/math].
Substituindo esse valor em cada expressão temos:
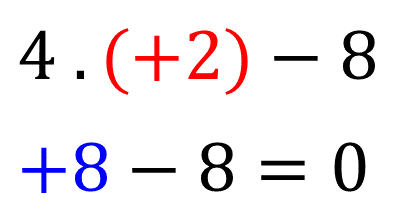
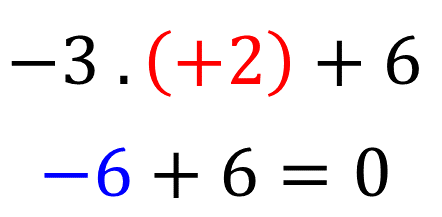
Como ambas tiveram o mesmo valor numérico dizemos que são equivalentes.
Se o valor a ser substituído na variável [math] k [/math] fosse [math] + \ 3 [/math] por exemplo.
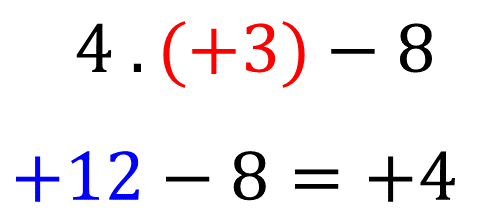
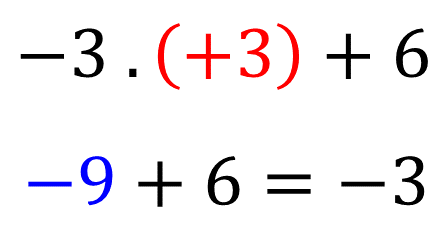
Para [math] k = + \ 3 [/math] os resultados foram diferentes, então para esse valor, afirmamos que as expressões não são equivalentes.
A linguagem algébrica
Linguagem algébrica é uma forma de modelar situações da vida cotidiana ou da natureza em linguagem matemática.
Observe a frase:
"O meu patrimônio dobrou em seis meses."
Nela, a palavra "dobrou" pode ser representada em linguagem matemática e seria escrita [math] 2x [/math].
Explicando melhor, dois significa o dobro e a letra [math] x [/math] é a variável que indica o que foi dobrado, o patrimônio.
São infinitas as expressões que podem ser traduzidas ou modeladas para a linguagem matemática.
Vejamos algumas muito comuns:
Um número ou uma quantidade [math] \rightarrow [/math] [math] x [/math]
O triplo de um número [math] \rightarrow [/math] [math] 3x [/math]
A terça parte de uma quantidade [math] \rightarrow [/math] [math] {x} \over {3} [/math]
O sucessor de um número [math] \rightarrow [/math] [math] x + 1 [/math]
O antecessor de um número [math] \rightarrow [/math] [math] x – 1 [/math]
O triplo do quadrado de uma quantia [math] \rightarrow [/math] [math] 3x^ {2} [/math]
A soma de dois números [math] \rightarrow [/math] [math] x + y [/math]
O quadrado da soma de dois números [math] \rightarrow [/math] [math] (x + 2)^ {2} [/math]
A soma dos quadrados de dois números [math] \rightarrow [/math] [math] x^ {2} + y^ {2} [/math]
Essas são só algumas das expressões que costumam aparecer em problemas de álgebra.
Conforme eles forem aparecendo, vamos aprendendo outras formas de representação.
Como viram, as expressões algébricas facilitam bastante os estudos de álgebra.
No próximo tópico vamos aprender ainda mais sobre tudo isso com o entendimento das equações.
Vamos praticar agora?
"A matemática pura é, à sua maneira, a poesia das ideias lógicas.”
Albert Einstein
Resolva as cruzadas abaixo para ajudar a fixar a teoria.
Resolva os seguintes exercícios abaixo para ajudar a fixar a parte prática.
1) Reduzindo os termos semelhantes na expressão [math] ab^ {2} - 3bc + 2ab + 10bc - 8 [/math] obtemos:
2) O valor numérico da expressão [math] 3p^ {2} q^ {3} - 4k [/math]; para [math] p = - 1 [/math], [math] q = - 2 [/math] e [math] k = 3 [/math] será igual a?
3) O produto de [math] (-54x^ {10} y^ {37}) [/math] por [math] (+17x^ {23} y^ {12} z) [/math] será?
4) Verifique se as expressões [math] x^ {2} - 4 [/math] e [math] x + 2 [/math] são equivalentes para [math] x = 3 [/math]
5) Escreva em linguagem algébrica a seguinte frase: A metade do cubo do quíntuplo de uma quantidade mais dezessete.

