As Sequências

As sequências são muito frequentes na matemática e estão mais próximas de nós do que imaginamos. Agora você terá a oportunidade de aprender um pouco mais sobre elas.
Introdução
Ao nosso redor inúmeras situações apresentam padrões. Várias situações do nosso cotidiano ou na própria natureza, podem ser identificados a partir de um item anterior, uma ordem e um comportamento específico. Chamamos de sequências as situações que podem ser descritas com essas características.
A todo momento lidamos com sequências. A rotina do dia, cada atividade realizada, cada tarefa ocorre em sequência. Acordar pela manhã, ir ao banheiro, escovar os dentes, lavar o rosto, trocar de roupas e tomar café é uma sequência que ocorre com frequência ao acordar.
Pode haver algumas pequenas mudanças para uma ou outra pessoa mas a maioria dessas tarefas são realizadas de manhã. Poderíamos considerar um padrão que os humanos possuem após acordar pela manhã.
A busca e o estudo pelas sequências tem justamente a finalidade de descobrir ou se aproximar ao máximo de um padrão com a intenção de prever os acontecimentos.
Existem algumas sequências muito importantes para a matemática. Vamos aprender agora sobre elas e também descobrir e interpretar como são definidas.


Quando as sequências são formadas apenas por números são chamadas de numéricas. Este é o tipo mais comum encontrado na matemática. Observe as seguintes sequências numéricas:
[math](0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20)[/math]
[math](1, 3, 5, 7, 9, 11, 13, 15, 17, 19, ...)[/math]
Todas são formadas somente por números. A primeira é classificada como uma sequência finita pois não tem continuidade. Ela é chamada de sequência dos números pares menores que [math] 22 [/math].
Já a outra sequência é classificada como sequência infinita. As reticências demonstram que existe continuidade. Ela será chamada de sequência dos números ímpares.
Existem inúmeras sequências numéricas conhecidas, como a sequência dos números primos, a sequência dos números quadrados perfeitos, etc.
Lei de formação de uma sequência
Muitas sequências numéricas poderão ser representadas por uma expressão algébrica. Esta expressão é definida como a lei de formação da sequência. Vamos ver como isso funciona.
Vamos usar uma letra [math] {a} [/math] seguida de um número que vai indicar a posição do termo na sequência. Nada impede o uso de outras letras como [math] b, c, d, e [/math] , por exemplo. Aqui utilizaremos a letra [math] a [/math] apenas por padrão de explicação.
Dessa forma, um termo qualquer da sequência será chamado de termo genérico ou generalizado. Será representado desta forma [math] a_ {n} [/math], onde a letra acima escolhida (aqui no caso a letra a), indicará o elemento genérico seguido de outra letra abaixo (aqui a letra [math] n [/math]). Esta última, será chamada de índice e indicará somente a posição que esse elemento ocupa na sequência.
Termos antecessores a [math] a_ {n} [/math] , sempre que necessários, serão identificados por [math] a_ {n - 1} [/math], [math] a_ {n - 2} [/math], [math] a_ {n - 3} [/math], e assim sucessivamente. Da mesma forma, termos sucessores serão identificados por [math] a_ {n + 1} [/math], [math] a_ {n + 2} [/math] , [math] a_ {n + 3} [/math].
Tomando a sequência de Fibonacci, vamos agora descrever esse padrão em matemática.
Seja um elemento qualquer em uma sequência posicionada na quarta posição. Podemos representá-lo por [math] a_ {4} [/math] onde a letra a indica o elemento e o número quatro a sua posição.
Tomamos como exemplo, uma sequência numérica iniciada por [math] a_ {0} [/math]. Aqui precisamos somente estar atentos ao índice se for solicitado o valor de posição do termo. Vejamos como é montada a sua lei de formação.
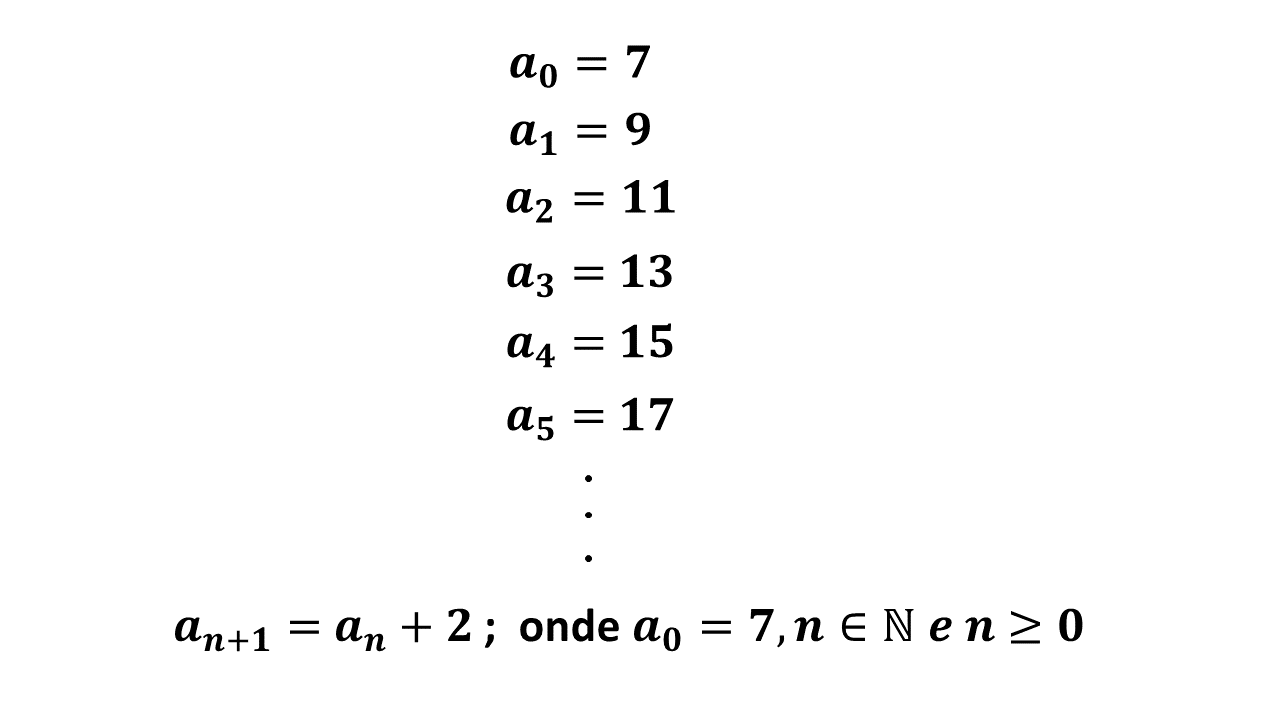
Como é possível ver, o valor de [math] a_ {0} [/math] é fixo. Portanto, a partir de [math] a_ {1} [/math] é que realmente a lei de formação começa a funcionar.
Para não haja problemas com a interpretação algébrica, lembre-se da forma genérica de representação para sucessores e antecessores de [math] a_ {n} [/math].
Podemos então interpretá-la da seguinte maneira: A partir de [math] a_ {1} [/math] ,cada novo termo inserido na sequência será igual a soma do seu antecessor somado a duas unidades.
Na última linha, essa lei de formação é descrita em linguagem matemática.
Outros tipos de sequências
Existem uma infinidade de tipos de sequências. Algumas delas possuem mais de uma classificação. Em outras páginas você vai conhecer outras dessas classificações importantes como as sequências recursivas, as não recursivas, as lógicas e as figurais.
Agora pratique um pouco!
"O importante é entender profundamente as coisas e as relações entre elas. É nisso que reside a inteligência.”
Laurent Schwartz
1) Determine a lei de formação responsável pela seguinte sequência numérica: [math] (5, 11, 17, 23, ...) [/math]
2) Determine os 5 primeiros termos da sequência numérica cuja lei de formação é dada por [math] a_ {n} = n^ {2} - 1 [/math], onde [math] n \in \mathbb {N} [/math] e [math] n \geq 1 [/math]
3) Sabendo que [math] a_ {1 } = 19, a_ {2} = 43 [/math] e [math] a_ {3} = 67 [/math] podemos afirmar que o elemento [math] a_ {7} [/math] dessa sequencia será?
4) Determine os 3 primeiros termos da sequência numérica cuja lei de formação é dada por [math] a_ {n} = n^ {3} + 1 [/math], onde [math] n \in \mathbb {N} [/math] e [math] n \geq 1 [/math]
5) Determine a lei de formação responsável pela seguinte sequência numérica: [math] (254, 458, 662, ...) [/math]

