As equações do 1º grau
com uma incógnita
Marcelo é um estudante focado e esforçado. Num final de semana lembrou que precisaria fazer uma revisão e um resumo sobre as equações do primeiro grau, assunto que havia aprendido recentemente. Não tinha a menor ideia de como iria começar, quando de repente ouviu uma voz que o deixou bastante surpreso.

"Fala ai Marcelo, tudo bem?" Perguntou a voz num tom amigável.
"Estou vendo que esta meio preocupado e parece perdido. Posso te ajudar?" Continuou a voz.
Totalmente paralisado, Marcelo respondeu: " Bem acredito que sim, não tem problemas, toda a ajuda é bem válida mas com quem estou falando por favor?"
Então a voz respondeu: "Sou simplesmente o narrador da sua história Marcelo."
"Mas como assim o narrador da minha história?" Retrucou Marcelo. "Não posso lhe ver? Isso é real?" Questionou mais uma vez, ainda embasbacado.
"Relaxa amigo!" Retornou a voz com bastante intimidade. "Deixa eu te guiar nesse desafio e verá. Não vai se arrepender."
"Bem, acho que não tenho muita escolha. Então vamos lá" Respondeu desconfiado.
"Assim que eu gosto de ver! Tudo vai ficar mais claro a partir de agora. Confie em mim! Vamos dar início ao assunto, respondendo a seguinte pergunta Marcelo."
O que são equações?


"A palavra equação esta relacionada a igualdade. Portanto, em matemática, equações são expressões algébricas que se relacionam por esta particularidade.
Assim, o objetivo ao resolver uma equação, será encontrar o elemento que a torna verdadeira."
"Só isso?" Respondeu Marcelo surpreso. "Não pode ser!"
"Sim meu caro amigo, esta é a simples definição de equação. Nada demais não é mesmo! Antes de começarmos a efetuar cálculos precisamos aprender mais um pouquinho da teoria. Nosso próximo passo será definir o seguinte:
Variável ou incógnita


"Uma pergunta muito importante nesse início de estudos Marcelo." Concluiu o narrador.
"Confunde mesmo! Se é importante, então vamos logo entender qual usar." Respondeu Marcelo.
"Veja bem, toda equação matemática é composta por letras e números. Todas as letras presentes em qualquer equação, serão chamadas de variáveis ou incógnitas. Quanto aos números presentes, nomeamos coeficientes."
Caso tenha mais dúvidas acesse o conteúdo expressões algébricas aqui no site para entender mais sobre o assunto.
"Continuando, a incógnita representa um elemento ou valor desconhecido que torna a equação (igualdade) verdadeira. Podemos ter equações com uma, duas, três incógnitas. Na verdade não há uma regra para a quantidade delas. Neste momento vamos estudar somente as equações que possuem apenas uma."
"Então Marcelo como esta indo bem te proponho um pequeno teste rápido antes de continuar, que tal?"
"Como assim sério? Já é possível responder questões só com esse nível de conhecimento?"
"Claro! Você não faz ideia. Convido todos os amigos estudantes que estejam acompanhando esta aula a fazerem esta revisão junto com o Marcelo."
"E ai Marcelo acertou todas?" Questionou o narrador
"Acertei uma e errei três, não tive um bom desempenho!"
"Não tem problema Marcelo, acontece. Depois releia tudo o que foi dito até o momento. Agora daremos mais um passo na sua revisão de equações. Vamos falar sobre o ..."
Grau de uma equação
"Pois bem Marcelo, saiba que toda incógnita terá um expoente. Quando estiver ausente, fica entendido que ele existe mas está apenas oculto. Como aprendemos em potenciação de números naturais, por favor dê uma revisada lá, este número oculto sempre será sempre o 1.
Uma equação que possui incógnita com expoente 1 (um) será chamada de equação do primeiro grau, se o expoente for o 2 (dois) será chamada de equação do segundo grau, sendo o 3 (três) o expoente do terceiro grau e assim por diante. Observe os exemplos abaixo."
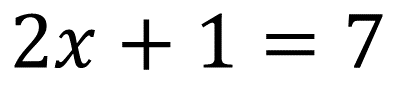
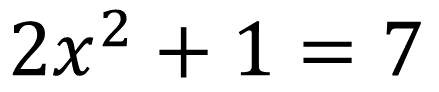
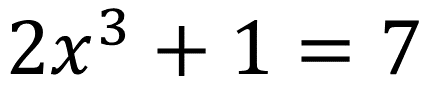
"Estamos revisando aqui apenas as equações do 1º grau e que possuem apenas uma incógnita."
"Nossa quanto detalhe!" Rebateu Marcelo.
"Pois é, observe esses detalhes nos exemplos abaixo. Veja esta expressão. O que você vê Marcelo?"
[math] 12(8 - 5) = 36 [/math]
"Vejo números e símbolos matemáticos. Uma expressão resumindo."
"Isso mesmo, muito bom! Neste caso, temos aqui apenas uma expressão numérica. Apesar de ser uma igualdade, não temos uma variável para tentar encontrar o valor. Observe agora esta outra. E agora? O que você vê?"
[math] 2 [/math][math] x [/math] [math] - 3 [/math][math] y [/math] [math] = 1 [/math]
"Novamente uma expressão só que agora com duas letras diferentes." Respondeu rapidamente Marcelo."
"Excelente observação! acima temos um exemplo de uma equação do 1º grau com duas incógnitas. Ficou claro? Este tipo de equação não é objeto ainda de nosso estudo. Agora observe atentamente mais este exemplo."
[math] x [/math] [math]- 5 = - 11 [/math]
"O que você vê Marcelo desta vez?"
"Eu vejo mais uma expressão com letras e números, sendo que desta vez só contém a letra [math] x [/math]."
"Exato! Esta sim é uma equação do 1º grau com apenas uma incógnita. Como explicado anteriormente, o objetivo aqui será encontrar o número oculto representado por esta letra."
Para conferir se o resultado está correto, basta substituir o valor encontrado para a variável na equação.
[math] 22 [/math] [math] + 15 = 37 [/math]
"Veja que a igualdade se confirma. Assim, afirmamos que o número 22 é solução da equação.
Representamos este conjunto solução (aqui representado pela letra S maiúscula) da seguinte forma: [math] S = \{ 22 \} [/math]." Concluiu o narrador.
"Realmente muita informação mas então é só isso? Perguntou Marcelo suspeito.
"Falta pouco amigo!" Disse a voz. " Vamos entender só mais um assunto e terminamos. Vamos falar rapidamente agora sobre...
Equações equivalentes
"Veja bem Marcelo a definição é a seguinte: equações do 1º grau que possuem o mesmo conjunto solução são chamadas de equações equivalentes. Simples né? Observe atentamente as duas equações abaixo e suas soluções."
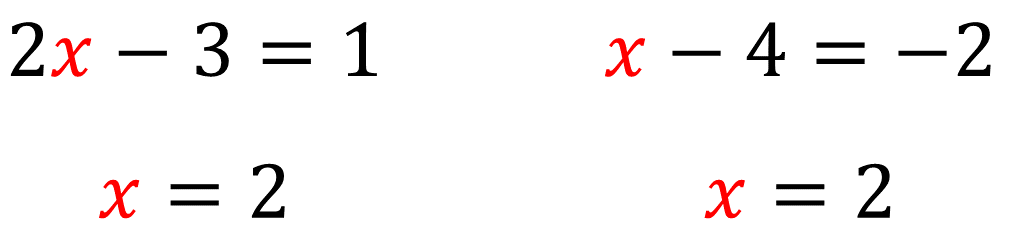
"Acima temos duas equações do 1º grau que possuem o mesmo valor para a variável [math] x [/math]. Pela definição, as duas equações são consideradas equivalentes."
"Ah essa foi fácil! Então quer dizer que só é preciso encontrar as raízes de duas ou mais equações e comparar se os resultados são iguais?" Disse Marcelo eufórico por ter visto a facilidade do tópico.
"Isso mesmo, parabéns! Para encerrar só é preciso dizer ainda que existem dois importantes princípios que serão estudados separadamente e que auxiliam nos cálculos de uma equação. São chamados de princípios da igualdade. Temos o princípio aditivo e o princípio multiplicativo."
"Olha adorei sua ajuda! Desculpe mas, qual seu nome mesmo? poderemos nos ver pessoalmente?"
"Foi um prazer caro amigo, até a próxima" Interrompeu a voz!
"Espera!" Disse Marcelo.
E assim por uns minutos ficou o silêncio e Marcelo boquiaberto mergulhado em seus pensamentos, espantado pelo ocorrido e maravilhado por ter apreendido tanto.
Vamos praticar?
"A beleza da matemática só se mostra aos seguidores mais pacientes."
Maryam Mirzakhani
1) O que quer dizer variável ou incógnita?
2) Encontre o valor da variável [math] y [/math] mentalmente sem resolver a equação [math] y + 4 = - 8 [/math] ; sendo [math] U = \mathbb {R} [/math]
3) Encontre o conjunto solução para a equação [math] x - 8 = 17 [/math] ; sendo [math] U = \mathbb {Z} [/math]
4) O que pode-se afirmar sobre as raízes das equações [math] 3x = 33 [/math] e [math] 5x = 55 [/math], sabendo que para ambas o valor encontrado é [math] 11 [/math]?
5) Qual o grau da equação [math] 218x + 346 = 564 [/math] no conjunto universo dos números naturais?


