Operações com ângulos
(adição)
Chegou o momento de aprender um pouco mais sobre o sistema sexagesimal, conhecer algumas operações (começaremos com a soma de ângulos) e saber o que é a bissetriz de um ângulo.
Introdução

Uma vez em uma aeronave, uma dupla de pilotos precisava seguir a seguinte instrução no manual de voo.
Vocês se encontram a [math] 42 ^{°} 19 ^{'} 38 ^{"}[/math] latitude norte e [math] 72 ^{°} 34 ^{'} 55 ^{"}[/math] longitude oeste. Para chegar ao seu destino deverão somar a essas coordenadas respectivamente [math] 22 ^{°} 09 ^{'} 15 ^{"}[/math] latitude norte e [math] 28 ^{°} 13 ^{'} 21 ^{"}[/math] longitude oeste.
Quais as coordenadas do destino para os pilotos? Ao final desta página você será capaz de efetuar este tipo de cálculo sem problemas. Antes vamos conhecer alguns assuntos importantes.
Bissetriz de um ângulo
Bissetriz de um ângulo é a reta que divide o ângulo exatamente ao meio, ou seja em duas partes iguais.

Na figura acima o segmento [math] \overline {OD} [/math] foi destacado como sendo uma bissetriz. Como consequência disso, ele dividiu o ângulo [math] A \widehat {O} B [/math] em dois ângulos iguais de medida [math] \alpha [/math].
Sistema sexagesimal
A unidade de medida mais utilizada nos dias atuais para medir ângulos chama-se grau. O símbolo que representa esta unidade é o seguinte: ( º )
Este símbolo sempre será posicionado logo acima do número que representará a amplitude.
Os ângulos não possuem medidas inteiras, possuindo então submúltiplos. Eles serão chamados de minuto ( ' ) e o segundo ( " ).
Assim temos as seguintes equivalências:
[math] 1 ^{°} \longrightarrow 60 ^{'}[/math]
[math] 1 ^{'} \longrightarrow 60 ^{"} [/math]
Cuidado aqui pois, apesar da semelhança, não estamos falando do minuto e segundo submúltiplos da hora como vimos em medidas de tempo. A representação nesse caso é bem diferente. Temos então o minuto e segundo para a hora e o minuto e segundo para ângulos.
É importante recordar que a medida de 1º (um grau) equivale a [math] \frac {1} {360} [/math] de uma volta completa na circunferência.
Agora com o entendimento do que é uma bissetriz de um ângulo e as equivalências no sistema sexagesimal para ângulos, podemos começar a realizar cálculos.
Operações com ângulos
É bem simples operar com ângulos e seus submúltiplos. Devemos calcular normalmente cada unidade separada, por exemplo, grau com grau; minutos com minutos e segundos com segundos
Após efetuados os cálculos, se possível, efetuamos conversões aplicando as equivalências mencionadas anteriormente. Vejamos cada uma delas agora com exemplos.
Adição de ângulos
Vamos começar efetuando a soma de alguns ângulos. Observe a figura abaixo.

Nela temos três ângulos, são eles: [math] F \widehat {O} G [/math], [math] G \widehat {O} H [/math] e [math] H \widehat {O} E [/math] com as respectivas medidas [math] m (F \widehat {O} G) = 20 ^{°} 15 ^{'} 25 ^{"} [/math], [math] m (G \widehat {O} H) = 18 ^{°} 07 ^{'} 08 ^{"} [/math] e [math] m (H \widehat {O} E) = 32 ^{°} 29 ^{'} 17 ^{"} [/math].
Começamos posicionando múltiplo e submúltiplos semelhantes um abaixo do outro.
[math] 20 ^{°} 15 ^{'} 25 ^{"}[/math]
[math] 18 ^{°} 07 ^{'} 08 ^{"}[/math]
[math] \underline {+ \ 32 ^{°} 29 ^{'} 17 ^{"}}[/math]
Agora efetuamos as somas unidade por unidade.
[math] 20 ^{°} 15 ^{'} 25 ^{"}[/math]
[math] 18 ^{°} 07 ^{'} 08 ^{"}[/math]
[math] \underline {+ \ 32 ^{°} 29 ^{'} 17 ^{"}}[/math]
[math] 70 ^{°} 51 ^{'} 50 ^{"}[/math]
Vamos a mais um exemplo com a adição. Dessa vez, vamos efetuar a soma de ângulos na imagem abaixo.
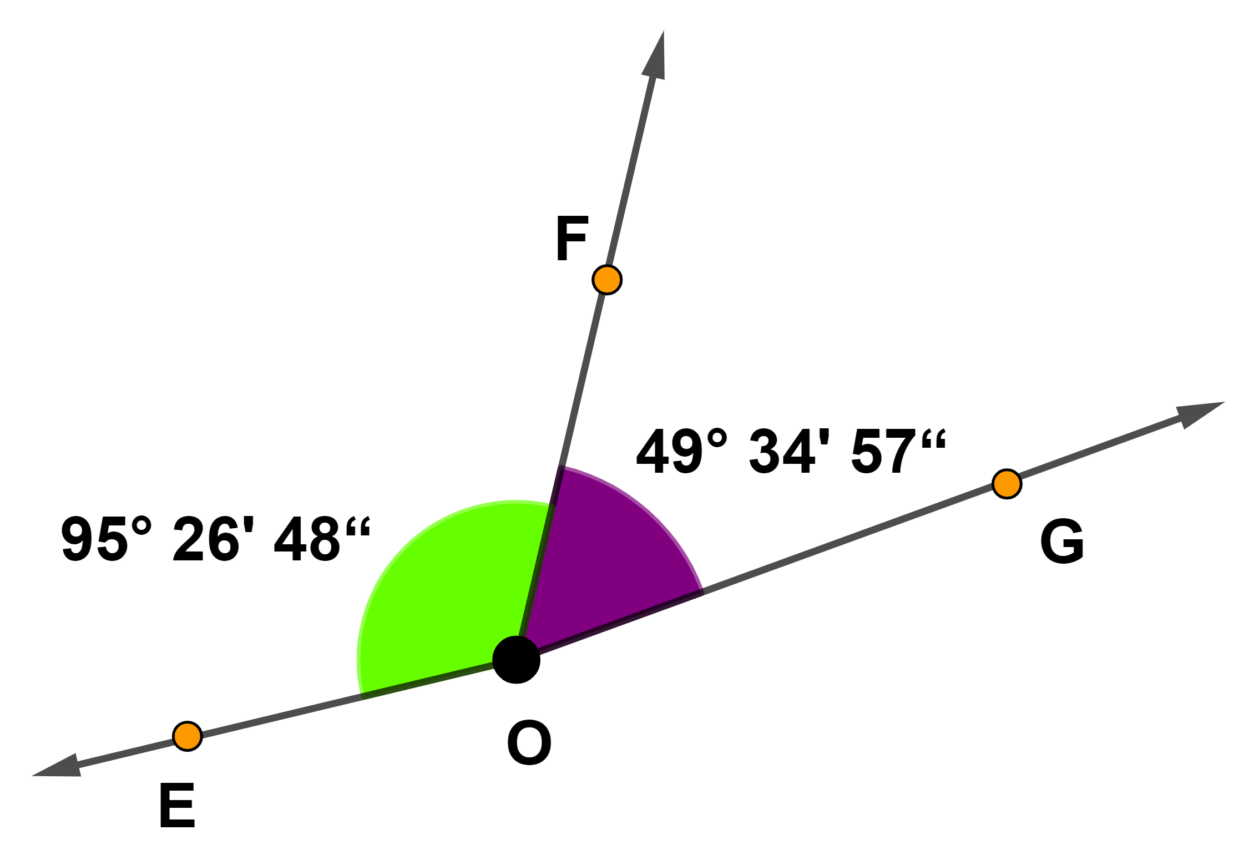
Adotaremos o mesmo procedimento de colocar as unidades semelhantes uma acima da outra.
[math] 95 ^{°} 26 ^{'} 48 ^{"}[/math]
[math] \underline {+\ 49 ^{°} 34 ^{'} 57 ^{"}}[/math]
Como fizemos no primeiro exemplo, somando unidade com unidade encontramos:
[math] 95 ^{°} 26 ^{'} 48 ^{"}[/math]
[math] \underline {+\ 49 ^{°} 34 ^{'} 57 ^{"}}[/math]
[math] 144 ^{°} 60 ^{'} 105 ^{"}[/math]
Será necessário dar continuidade com a soma de ângulos pois, os submúltiplos apareceram com valores iguais ou maiores que 60. Logo, vamos converter cada unidade começando pelos segundos.
Se [math] 60 ^{"} \longrightarrow 1 ^{'} [/math]
então [math] 105 ^{"} \div 60 = 01^{'} 45^{"} [/math]
[math] 144 ^{°} 60 ^{'} 00 ^{"}[/math]
[math] \underline {+ \ 00 ^{°} 01 ^{'} 45 ^{"}}[/math]
[math] 144 ^{°} 61 ^{'} 45 ^{"}[/math]
Observe que mudamos [math] 105 ^{"} [/math] para [math] 00 ^{"} [/math] para ficar mais visível a conversão. O mesmo fazemos ao converter os [math] 60 ^{'} [/math]. Juntamos o [math] 1 ^{'} [/math] encontrados nos segundos pelo cálculo anterior e efetuamos então a divisão de [math] 61 ^{'} [/math] por 60 novamente.
Se [math] 60 ^{'} \longrightarrow 1 ^{°}[/math]
então [math] 61 ^{'} \div 60 = 01^{°} 01^{'} [/math]
[math] 144 ^{°} 00 ^{'} 45 ^{"}[/math]
[math] \underline {+ \ 01 ^{°} 01 ^{'} 00 ^{"}} [/math]
[math] 145 ^{°} 01 ^{'} 45 ^{"}[/math]
Por fim, depois de todas as somas e conversões, encontramos o resultado final.
Retomando o problema da soma de ângulos
Lembra do nosso problema inicial? Então agora como tinha dito, poderemos encontrar a solução tranquilamente. Portanto vamos somar! Começaremos pelas latitudes:
[math] 42 ^{°} 19 ^{'} 38 ^{"}[/math]
[math] \underline {+\ 22 ^{°} 09 ^{'} 15 ^{"}} [/math]
[math] 64 ^{°} 28 ^{'} 53 ^{"}[/math]
No caso da soma das latitudes não precisou efetuar nenhuma conversão. Vamos então somar as longitudes:
[math] 72 ^{°} 34 ^{'} 55 ^{"}[/math]
[math] \underline {+\ 28 ^{°} 13 ^{'} 21 ^{"}} [/math]
[math] 100 ^{°} 47 ^{'} 76 ^{"}[/math]
Aqui precisamos converter os segundos já que o valor ficou acima de 60. Nesse caso:
Se [math] 60 ^{"} \longrightarrow 1 ^{'} [/math]
então [math] 76 ^{"} \div 60 = 01^{'} 16^{"} [/math]
E enfim somando encontramos:
[math] 100 ^{°} 47 ^{'} 00 ^{"}[/math]
[math]\underline {+\ 00 ^{°} 01 ^{'} 16 ^{"}}[/math]
[math] 100 ^{°} 48 ^{'} 16 ^{"}[/math]
Portanto os dois pilotos vão precisar seguir [math] 64 ^{°} 28 ^{'} 53 ^{"} [/math] latitude norte e [math] 100 ^{°} 48 ^{'} 16 ^{"} [/math] longitude sul para chegar corretamente ao destino.
Vamos praticar?
"A felicidade não é uma constante matemática, mas pode alcançar o infinito em um dado momento."
Fabrício Britto
Continue praticando!
Gostaria de continuar praticando com mais exercícios como do questionário acima?
Se já for inscrito, faça login e procure pela página testes online para acesso imediato.
Agora caso ainda não seja cadastrado aqui no site, clique no botão logo abaixo, cadastre-se e tenha também acesso a algumas de nossas listas disponíveis.

