As Relações entre ângulos
Dessa vez veremos algumas relações entre ângulos.
Introdução
Carolina trabalha na construção civil e a todo momento se depara com esboços e medidas de ângulos em plantas de construção. Ela usa com muita frequência régua, compasso, esquadros e também o transferidor.
Um dia durante um de seus trabalhos, Carolina se deparou com algumas questões.
Precisava preencher com cores diferentes determinadas regiões no desenho e para isso deveria utilizar dois ângulos. Surgiu então a dúvida se precisaria usar dois ângulos agudos, dois ângulos obtusos, dois côncavos ou se na verdade deveria usar um de cada, como um obtuso e um agudo, um côncavo e um obtuso, etc.
Depois de analisar algumas instruções, descobriu que os dois ângulos deveriam somar 180º. Foi aí então que ela lembrou de suas aulas de matemática na escola e percebeu que precisaria recordar o assunto chamado relações entre ângulos.
Quais os tipos de ângulos que devem ser usados no projeto? Qual o nome da relação entre eles? Ao final da página você terá todas essas questões respondidas. Vamos então recordar agora com a Carolina cada uma dessas relações.
Ângulos complementares
Essa relação afirma que dois ou mais ângulos são chamados complementares se a soma de suas medidas for igual a 90°.
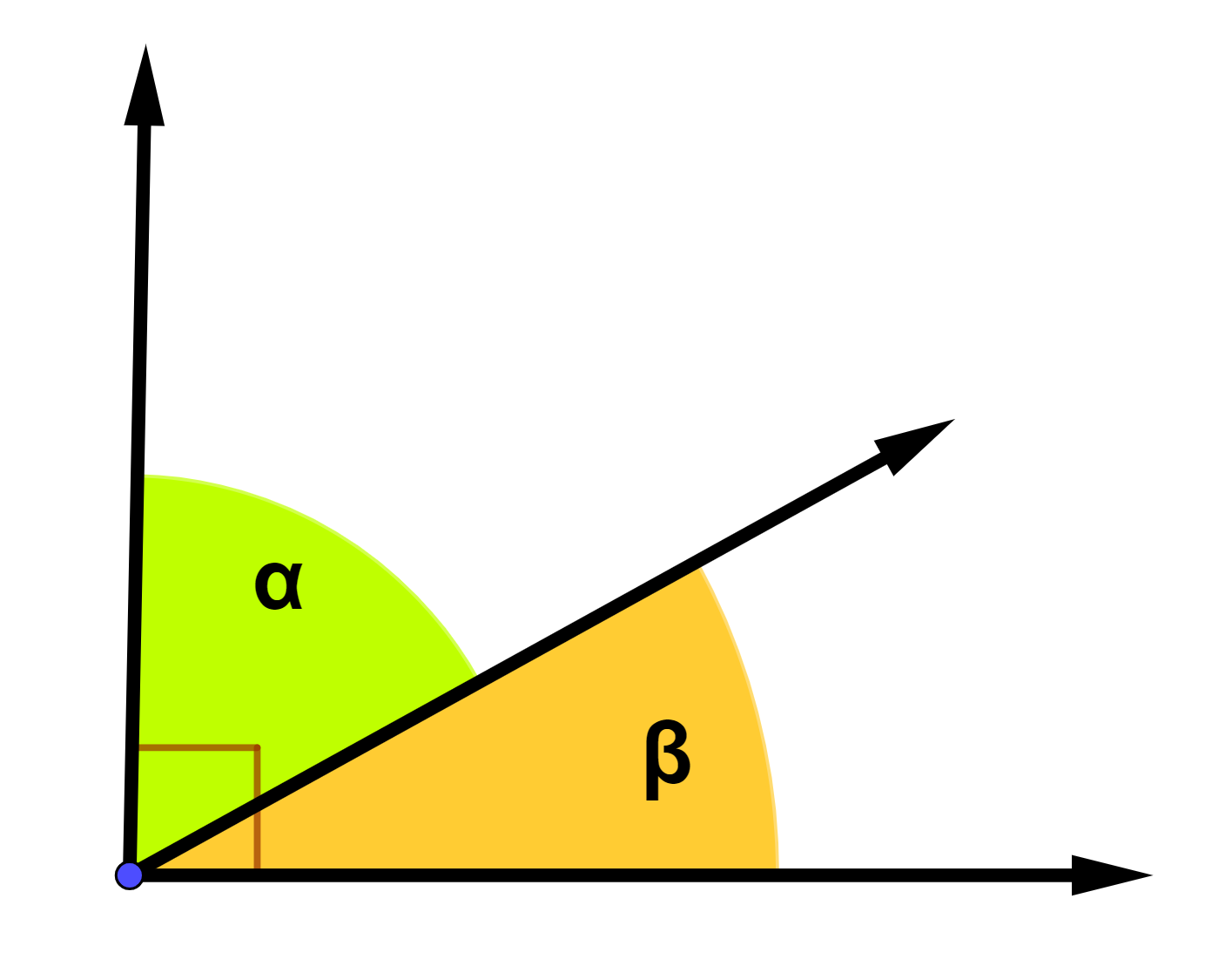
[math] α + β = 90° [/math].
Observações:
- Dizemos também que a soma é igual a um reto.
- Todos os ângulos sempre serão agudos.
Exemplo:
Qual o complemento de [math] 35° [/math]?
Resposta: [math] 55° [/math]
Já que [math] 35° + 55° = 90° [/math]
Ângulos suplementares
Esta outra relação, afirma que dois ou mais ângulos são chamados suplementares se a soma de suas medidas for igual a 180°.

[math] α + β = 180° [/math].
Observações:
- Dizemos também que a soma é igual a um raso.
- Dois ângulos retos são suplementares.
- A soma pode ser dada por pelo menos um ângulo obtuso e os demais agudos.
Exemplo:
Qual o suplemento de [math] 97° [/math]?
Resposta: [math] 83° [/math]
Já que [math] 97° + 83° = 180° [/math]
Ângulos replementares
Esta relação afirma que dois ou mais ângulos são chamados replementares se a soma de suas medidas for igual a 360°.

[math] α + β = 360° [/math].
Observações:
- Dizemos também que a soma é igual a um ângulo de uma volta completa.
- Dois ângulos rasos são replementares.
- Quatro ângulos retos são replementares.
- A soma pode ser dada por um ângulo côncavo e um ângulo agudo ou ainda por um ângulo côncavo e outro obtuso.
Exemplo:
Qual o replemento do ângulo de [math] 25° [/math]?
Resposta: [math] 335° [/math]
Já que [math] 25° + 335° = 360° [/math]
Ângulos explementares
Por fim, esta última relação afirma que dois ou mais ângulos são chamados de explementares se a diferença de suas medidas for igual a 180°.
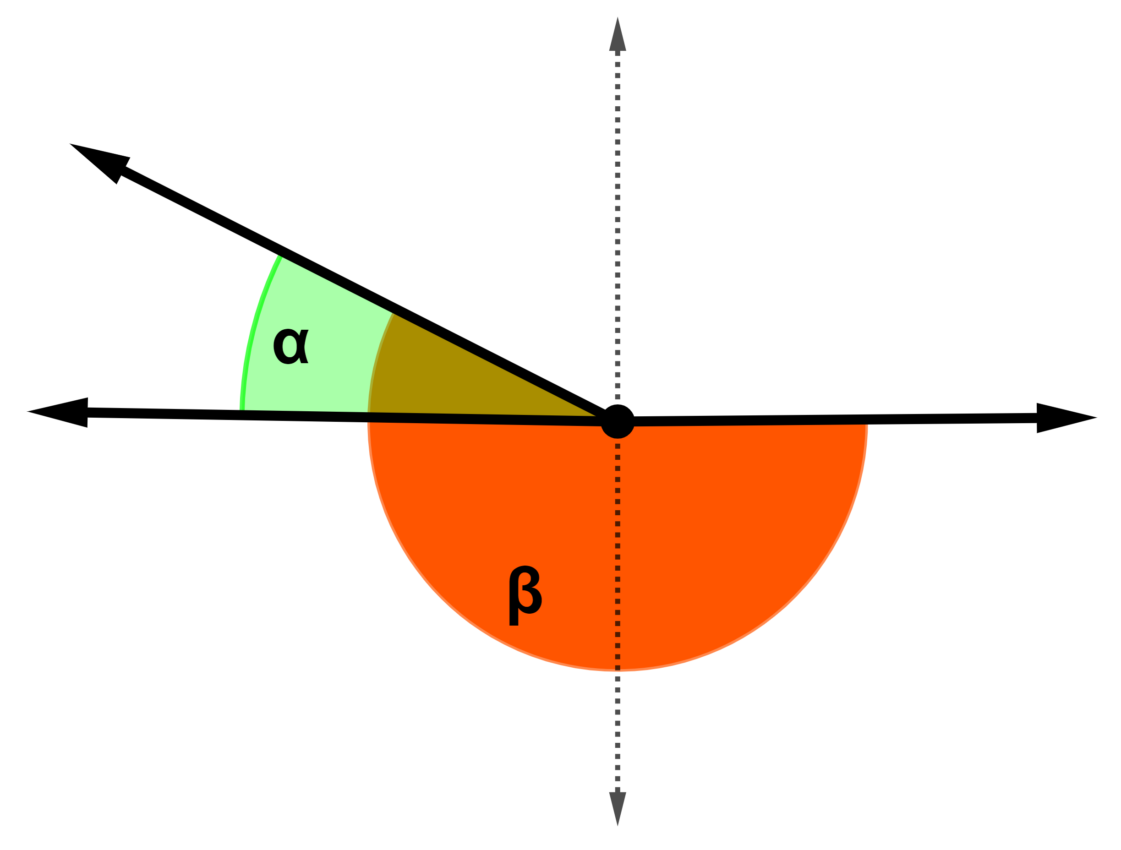
[math] β - α = 180° [/math].
Observações:
- Dizemos também que a diferença é igual a um raso.
- A diferença pode ser dada por um ângulo côncavo e um ângulo agudo.
- A diferença pode ser dada por um ângulo côncavo e um ângulo obtuso.
Exemplos:
Qual o explemento do ângulo de [math] 256° [/math]?
Resposta: [math] 76° [/math]
Já que [math] 256° - 76° = 180° [/math]
Qual o explemento do ângulo de [math] 359° [/math]?
Resposta: [math] 179° [/math]
Já que [math] 359° - 179° = 180° [/math]
Usando as relações entre ângulos para solucionar o problema da Carolina
Lembra da Carolina? Conseguiu identificar qual das relações acima ela vai precisar trabalhar em seu projeto? Bem, se você respondeu ângulos suplementares acertou! Parabéns!
Respondendo a outra questão, no caso desse projeto, será necessário fazer uso de um ângulo obtuso e outro agudo. Prontinho agora ficou fácil. Basta agora decidir quais as melhores medidas que vão se adequar ao que precisa. Então mãos à obra Carolina! Sucesso!
E quanto a você? Gostaria de exercitar um pouquinho pra ter certeza se assimilou mesmo o conteúdo?
Vamos praticar?
"Suba o primeiro degrau com fé. Não é necessário que você veja toda a escada, apenas dê o primeiro passo."



