Os Ângulos
Sem o estudo e conhecimento dos ângulos fica muito difícil aprender geometria. Consegue imaginar a presença deles no seu dia a dia? Olhe com atenção a sua volta! Acredite, estão por toda parte. Então vamos juntos explorar agora este tema surpreendente!
Introdução
Os ângulos podem ser encontrados em diferentes lugares: na natureza, nas construções, bem como em muitas coisas que observamos e utilizamos no nosso cotidiano.
Mas afinal, o que são ângulos?
Ângulo é o nome dado a região entre duas semirretas que partem de uma mesma origem.

Notação matemática de ângulos
O ponto comum aos dois lados é o vértice desse ângulo. Este ponto será comumente representado por uma letra maiúscula do alfabeto ocidental (por se tratar de um ponto) acompanhado do acento circunflexo.
No caso da imagem abaixo, o vértice pode ser identificado como o ponto O.

Cada lado do ângulo poderá ser escrito de acordo com a nomenclatura utilizada para representação de uma semirreta. Você já deve ter um conhecimento desta forma de representação mas se ainda não viu nada sobre esse assunto, pode acessar o tópico introdução a geometria plana que irá encontrar tudinho lá.
Na figura acima podemos identificar esses dois lados como a semirreta [math] \overrightarrow {OA} [/math] e a semirreta [math] \overrightarrow {OB} [/math].
Colocando essas duas semirretas e o vértice (origem de cada lado) num mesmo símbolo, a representação desse ângulo será escrita [math] A\hat{O}B [/math].
Observe atentamente que a origem dos lados fica posicionado no centro, entre os outros dois pontos e com um acento circunflexo acima para afirmar que se trata de um ângulo. Muita atenção pois, é obrigatório esta forma de representação.
Amplitude de um ângulo
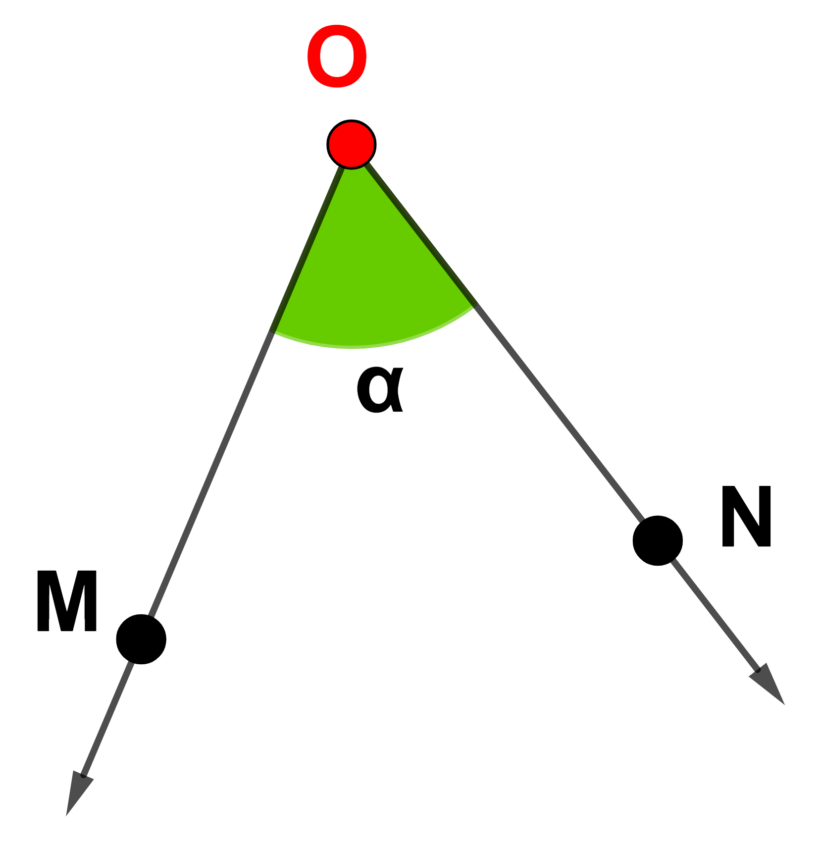
Comparando a imagem acima com a anterior, temos uma pequena mudança agora. Inserimos a letra grega alfa na região do ângulo para representar a sua amplitude ou medida.
A notação será a seguinte: [math] m (M\hat{O}N) = \alpha [/math]
Sistemas de medida de ângulos
Vamos falar agora dos dois sistemas utilizados para medir ângulos. É necessário ir se familiarizando com eles pois serão exigidos em muitos tópicos na matemática.
Sistema circular
No Sistema Internacional de unidades, temos como unidade padrão de medida de ângulos o radiano.
Quando temos uma circunferência de raio de medida r como na figura ao lado e destacamos um de seus arcos, cujo comprimento também é igual a r, dizemos que esse arco tem o comprimento igual a 1 radiano (rad).
A consequência disso é que a medida do ângulo central (aqui representado pela letra grega α) tem a mesma medida do arco destacado. Assim, podemos afirmar que este ângulo também possui a medida de 1 radiano.
Formalmente definimos radiano como sendo a razão entre o arco de uma de circunferência e seu raio.


Sistema sexagesimal
A unidade de medida mais utilizada nos dias atuais para medir ângulos chama-se grau. Seu uso facilita bastante a medição em diversas situações.
Durante muitos séculos, diversas civilizações antigas se utilizaram desta unidade para medir ângulos.
Os seus submúltiplos são o minuto ( ' ) e o segundo ("). Você poderá ter um entendimento mais aprofundado sobre as conversões e operações com o grau acessando o tema medidas de ângulo.
A medida de 1º (um grau) equivale a [math] \frac {1} {360} [/math] de uma volta completa na circunferência.
Relação entre radiano e grau
As unidades radiano e grau podem ser convertidas uma na outra. Para isso é necessário saber duas coisas:
1º) Saber que a fórmula que calcula o comprimento de uma circunferência é dada por C = 2πr.
2º) Saber também que uma volta completa na circunferência mede 360º.
Vamos agora a algumas conclusões.
Pela definição formal de radiano para um arco completo γ de uma circunferência temos o seguinte:
[math] γ = [/math] [math] \frac {C}{r} [/math]]
[math] γ = [/math] [math] \frac {2πr}{r} [/math]
[math] γ = {2π} \ rad [/math]
Com isso concluímos:
[math] 2π \ rad= 360^ {\circ} [/math]
[math] π \ rad= \frac {360^ {\circ}} {2} [/math]
[math] π \ rad= 180^ {\circ} [/math]
A partir dessa conclusão podemos converter qualquer ângulo entre as duas unidades.
Por exemplo, digamos que você queira converter 45º em radianos? Basta utilizar a fórmula [math] γ = \frac {α} {180} \cdot π [/math], onde [math] γ [/math] é a medida do ângulo em radianos e [math] \alpha [/math] é a medida dada em graus.
Veja:
[math] γ = \frac {α} {180} \cdot π [/math]
[math] γ = \frac {45} {180} \cdot π [/math]
Simplificando a fração
[math] γ = \frac {1} {4} \cdot π [/math]
[math] γ = \frac {π} {4} rad [/math]
Como medir um ângulo?
Geralmente para medir os ângulos na matemática utilizamos o transferidor. Trata-se de um instrumento em círculo ou semicírculo que é dividido respectivamente em 360 ou 180 graus.


Para usá-lo basta posicionar o centro do transferidor no local que será marcado como o vértice do ângulo e logo em seguida marcar a medida em graus desejada. Depois ligue esses pontos com a régua para determinar os lados ângulo. Instrumento realmente muito prático e fácil de manusear.
Outros instrumentos mais técnicos que auxiliam na medição de ângulos são o teodolito bastante utilizado na engenharia e o sextante utilizado na navegação náutica.


Vamos praticar um pouco?
“Mesmo que a jornada seja lenta, abrir mão não acelera”
Anônimo
Continue praticando!
Gostaria de continuar praticando com mais exercícios como do questionário acima?
Se já for inscrito, faça login e procure pela página testes online para acesso imediato.
Agora caso ainda não seja cadastrado aqui no site, clique no botão logo abaixo, cadastre-se e tenha também acesso a algumas de nossas listas disponíveis.

