Números primos
Chegou o grande momento de estudarmos os números primos. Vamos apreender suas características, pra que servem e também onde e como são utilizados.
Introdução

Numa tarde nublada de Outono, as amigas Ayumi e Niara caminhavam pelos jardins do colégio onde estudavam. Em um certo momento, Niara indagou Ayumi sobre o último assunto abordado na aula de matemática já que havia faltado as últimas duas aulas.
- Fala ai Ayumi, estou preocupadíssima! Preciso pegar o último conteúdo da aula de matemática o mais rápido possível. Teria como me ajudar?
- Vixi Niara, você ainda não pegou nada? O professor falou sobre os números primos sabia?
- Pois é, cheguei a ouvir o pessoal comentando. O que achou do assunto? Conteúdo muito difícil? Perguntou Niara.
- Olha Naira, eu particularmente achei tudo muito tranquilo. Ele explicou a teoria muito bem e até citou alguns exemplos de aplicação desses números. Achei a abordagem bem legal. Posso te passar o resumo de tudo bem rapidinho, gostaria de ver agora?
- Claro, claro! Respondeu Naira sorridente.
- Então vamos sentar ali naquele banco que vou te explicar amiga!

- Então amiga o professor foi bem direto. Ele falou sobre a importância dos números primos, suas características e também fez um breve comentário sobre a utilização deles na matemática e no nosso dia a dia, disse Ayumi.
- Estou bastante ansiosa amiga, por favor vamos bem devagar passo a passo tudo bem? Por onde devemos começar? Respondeu Naira.
- Claro! Você verá que o assunto é bem tranquilo. Vamos começar pela definição de número primo.
Definição de números primos
Um número natural [math] P [/math] diferente de zero e de um, será classificado como número primo quando possuir como divisores somente o número [math] 1 [/math] e ele próprio.
Ou seja, as únicas divisões exatas (aquelas que possuem resto zero) que um número primo pode ter são [math] P \div 1 [/math] e [math] P \div P [/math].
Muita atenção neste ponto Niara. Veja que há a necessidade das duas divisões existirem e não somente uma delas. Se isto ocorrer, o número natural não será considerado número primo. É o que acontece com os números zero e um. Eles não podem ser números primos já que zero não pode ser divisor de um número natural (ver divisão de um número natural) e o número um só tem a si próprio como divisor.
Em outras palavras, também é possível dizer que um número natural [math] P [/math] é dito primo quando não for possível escrevê-lo como o produto de dois números naturais [math] a [/math] e [math] b [/math] com [math] a > 1 [/math] e [math] b > 1 [/math].
Visto a definição acima, fica fácil identificar dentro deste conjunto os primeiros números primos que seriam os números [math] 2, 3, 5, 7, 11 … [/math]
- Bem tranquilo até Niara? Questionou Ayumi.
- Sim, respondeu Niara. Entendi perfeitamente o que determina se um número é ou não primo.
- Então quanto aos números que não forem classificados como números primos serão chamados de números compostos. Falaremos mais porque são chamados dessa forma mais a frente. Preciso comentar primeiro sobre um método bastante interessante que ele explicou para determinar alguns números primos.
Crivo de Eratóstenes
Olha Niara, o professor falou rapidamente sobre Eratóstenes. Contou que ele foi um excepcional matemático da Grécia antiga realizador de grandes descobertas. Chegou a ser considerado o segundo maior do mundo na época. É famoso por ter conseguido calcular o raio do nosso planeta e também determinou um método bastante eficaz para identificar números primos.
Este método pode ser facilmente utilizado na busca de números primos pequenos. Ele leva seu nome e é conhecido por crivo de Erastótenes. Vou exemplificá-lo buscando determinar quais são os números primos existentes de zero a cem.
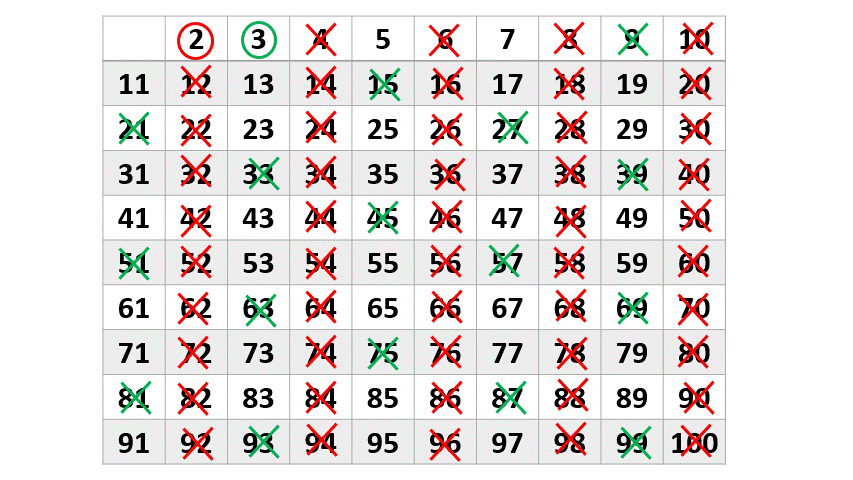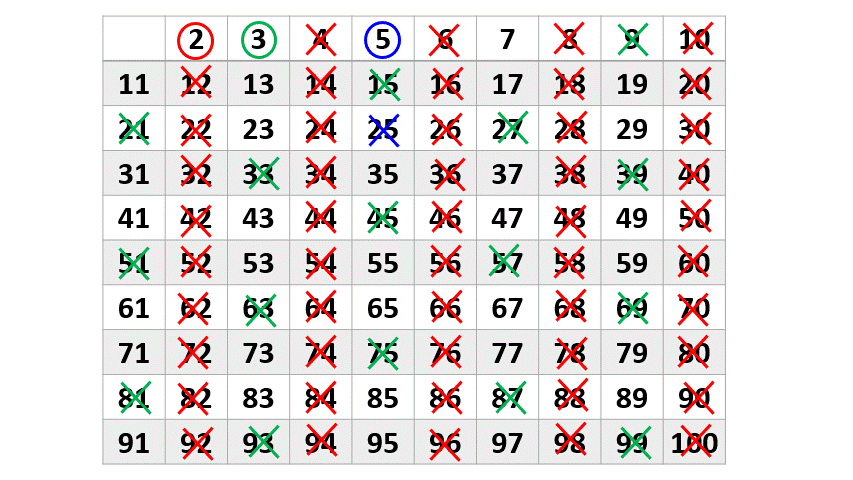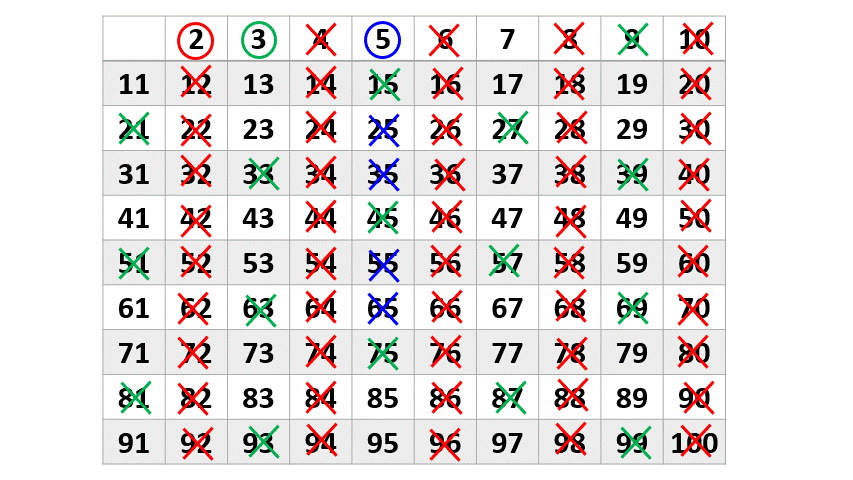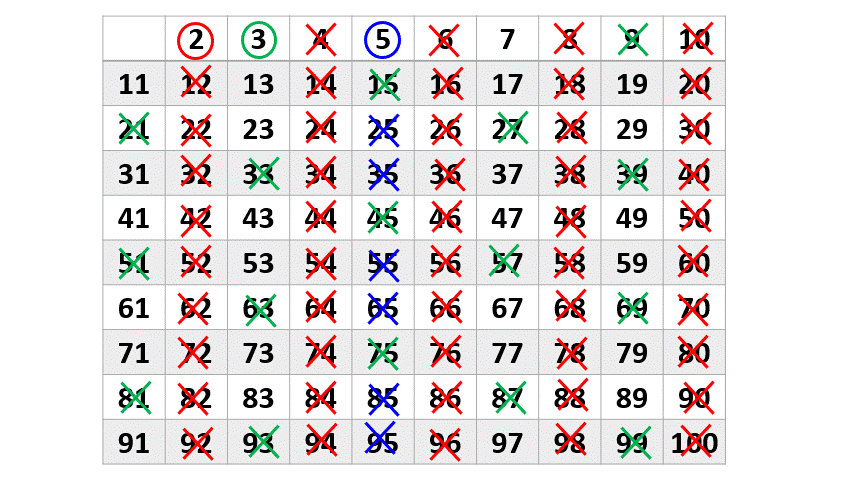
Este método consiste em ir marcando em ordem, os números primos um a um juntamente com seus múltiplos. Desse modo, primeiro em uma tabela, escrevemos os números de [math] 2 [/math] a [math] 100 [/math]. Marcamos o número [math] 2 [/math] com um círculo já que é o primeiro número primo. Em seguida, marcamos com um X, todos os seus múltiplos que serão descartados.

Repetimos todo o processo, sendo agora com o número [math] 3 [/math]. Perceba que alguns lá foram excluídos antes por também serem múltiplos de [math] 2 [/math]

Damos continuidade ao processo, marcando e excluindo dessa vez os múltiplos do próximo número primo o [math] 5 [/math] que ainda não foram marcados.
Ainda em continuidade com o nosso processo, precisamos continuar com a exclusão de múltiplos. Dessa vez faremos o próximo número primo, será o [math] 7 [/math].

Pronto! Chegamos ao final da nossa busca. Não precisaremos utilizar o próximo número primo, no caso o [math] 11 [/math] porque não há múltiplos dele a eliminar. Basta agora, formar o conjuntos dos números primos procurados.

Usando o Crivo de Erástotenos, encontramos os seguintes números primos entre [math] 2 [/math] e [math] 100 [/math]:
[math] \{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 57, 59, 61, 67, 71, 79, 83 , 89, 97\} [/math]
Teorema fundamental da aritmética
- Interessante a identificação de números primos utilizando o crivo de Eratóstenes não é mesmo Naira! - Indagou Ayumi
- Achei bem fácil Ayumi! Basta ter bastante atenção que não tem erro.
- Pois é amiga mas, agora vamos falar também dos números que não são primos os chamados compostos. Para iniciar esse assunto o professor falou sobre um importante teorema descoberto na antiguidade pelos matemáticos. Este teorema diz o seguinte:
Todo número natural maior que [math] 1 [/math] ou é primo ou pode ser escrito de forma única, como um produto onde os fatores são todos números primos.
- Nossa Ayumi! Isso é uma descoberta incrível. Então pelo que entendi, os números primos são a verdadeira base de todos os números? Assim como as células formam os seres vivos? Que interessante isso! Estou muito surpresa. Comentou Niara.
- É amiga isso mesmo! E este teorema já era sabido por muitos estudiosos na Grécia antiga conhecidos por pitagóricos. É demonstrado nas publicações dos livros de Euclides, outro grande matemático da época e mais tarde foi novamente demonstrado e corrigido por Gauss no século [math] XVI [/math].
- O TFA como costuma ser chamado é uma das mais poderosas ferramentas da matemática. Para um número composto ser escrito como um produto de fatores primos precisamos fazer a sua decomposição Niara. Todo o cálculo é realizado com o processo de decomposição em fatores primos.
Mais um conjunto infinito?
"Então Niara, mais uma curiosidade que o professor trouxe foi que o conjunto dos números primos é mais um conjunto infinito. Ele disse que essa afirmação foi provada por grandes matemáticos como Euclides, Dirichlet e Sierpinski. Disse que as demonstrações dessa afirmação serão mostradas em outro momento oportuno. Agora bastaria apenas saber que é verdadeira.
Com isso começou uma verdadeira corrida e surgiu muita curiosidade sobre como seria o próximo número primo e quem o encontraria. O maior número primo descoberto até o momento possui [math] 24.862.048 [/math] de dígitos e só possível sua descoberta devido aos poderosos métodos computacionais da atualidade."
Mas porque a intensa pesquisa em descobrir números primos tão grandes? Existe uma verdadeira caçada em busca de novos números hoje em dia utilizando centenas ou até milhares de computadores interligados em todo o planeta. Bem, o que se sabe isso é que tudo começou a base de muita curiosidade mesmo assim como tantos outros assuntos da matemática. A evolução da internet e da Criptografia que fez tudo mudar. Isto porque se mostraram bastante úteis e eficientes para a codificação de dados.
A Criptografia que é a ciência de codificar e decodificar dados através de algoritmos, utiliza um método conhecido por RSA que se mostrou bastante eficaz com o uso dos números primos. Fazendo um rápido resumo, sabe-se que este método trabalha utilizando o produto de números primos muito grandes para gerar chaves de código.
Quanto maior forem esses números mais complexo e demorado se torna o processo de tentar decodificar os dados caso alguém que não possua a chave de acesso tente quebrar o código.
Este método futuramente será melhor explicado e aprofundado em outra página aqui mesmo no site, fiquem atentos.
Números esfênicos
" Uma outra curiosidade trazida por ele foi a definição dos chamados números esfênicos. Ele explicou que são todos os números formados pelo produto de três números primos distintos. Vejamos alguns exemplos
O número [math] 30 [/math] é um número esfênico pois [math] 30 = 2 \times 3 \times 5 [/math]. Este é primeiro número esfênico.
O número [math] 42 [/math] é um outro exemplo de número esfênico já que [math] 42 = 2 \times 3 \times 7 [/math].
Disse ainda que todos esses números possuem exatamente 8 divisores.
Como um número esfênico [math] N [/math] será formado pelo produto dos primos [math] x . y . z [/math] então o conjunto de seus divisores será formado por [math] \{ 1, x, y, z, xy, xz, yz, xyz \} [/math]."
Um aprendizado enriquecedor

- Então Niara esse foi o resumo sobre os números primos. Como eu disse, o professor ficou de abordar ao logo do semestre mais conteúdo relacionado ao tema. Por enquanto é só isso mesmo, disse Ayumi.
- Amiga nem sei como lhe agradecer. Estou com uma plena sensação de alívio sabia. Olha, parabéns você explica muito bem! Disse Naira com um sorriso encantador.
- Ah que ótimo ouvir isso! Nesse caso amiga ficou ainda alguma dúvida sobre o assunto?
- Não , não, nenhuma dúvida!
- Então agora vou lhe passar alguns exercícios que o professor passou e pediu para praticar bastante.
Esse mesmo problema seria ainda mais rapidamente resolvido com a ajuda de outras ferramentas que aprenderemos mais a frente. Por ora, vamos praticar um pouco mais para fixar o aprendizado.
Hora de praticar um pouco!
"Todas as coisas são números."
Pitágoras
Continue praticando aqui!
Gostaria de continuar praticando com mais exercícios como do questionário acima?
Se já for inscrito, faça login e procure pela página testes online para acesso imediato.
Agora caso ainda não seja cadastrado aqui no site, clique no botão logo abaixo e cadastre-se para também ter acesso a mais algumas de nossas listas disponíveis.

