Equações do 1° grauutilizando o princípio aditivo

O princípio aditivo
Quando estudamos as equações do 1º grau, falamos rapidamente sobre o princípio aditivo que diz o seguinte:
Em toda igualdade, se adicionarmos ou subtrairmos um mesmo número em ambos os lados (membros) de uma equação, o resultado não se altera.
Vejamos com mais detalhes, alguns exemplos para melhorar nosso entendimento sobre o assunto e sua importância.
Princípio aditivo - Exemplo 1
Considere a seguinte equação:
[math] x + 19 = 27 [/math]
O primeiro passo é resolvê-la deixando a incógnita em apenas um lado (membro) da equação. Fazemos isso nesse exemplo adicionando o inteiro dezenove negativos aos dois membros da equação.
[math] x + 19 [/math] [math] -\ 19 [/math] [math] = 27 [/math] [math] -\ 19 [/math]
O próximo passo é efetuar todos os cálculos possíveis.
[math] x + 0 = 8 [/math]
Com isso, conseguimos obter em um lado da equação apenas a incógnita [math] x [/math]. Nesse caso encerramos nossa equação. Chegamos ao objetivo de encontrar o valor procurado da variável.
[math] x = 8 [/math]
Esse é um exemplo do uso do princípio aditivo. Vejamos mais um exemplo com um outro modelo de equação do 1º grau.
Prncípio aditivo - Exemplo 2
Seja agora a equação:
[math] 2x + 8 = x - 3 [/math]
Aqui neste caso, vamos primeiro eliminar a variável [math] x [/math] em um dos membros da equação adicionando [math] x \ negativo [/math] em ambos os lados desse jeito.
[math] 2x [/math] [math] - \ x [/math] [math] + \ 8 = x [/math] [math] - \ x [/math] [math] - 3 [/math]
Obtemos então o resultado.
[math] x + 8 = 0 - 3 [/math]
Pronto! Agora usamos novamente o princípio aditivo como no primeiro exemplo eliminando o número 8 em um lado da equação com o objetivo de termos a variável "sozinha" daquele lado. Para isso adicionamos o inteiro 8 negativos em ambos os lados.
[math] x + 8 [/math] [math] - \ 8 [/math] [math] = - \ 3 [/math] [math] - \ 8 [/math]
Como era de se esperar, temos o seguinte resultado.
[math] x + 0 = - 11 [/math]
Por fim chegamos a
[math] x = - 11 [/math]
Utilizando métodos práticos

Os dois exemplos acima mostram profundamente os detalhes, ou seja, o verdadeiro passo a passo dos cálculos que são efetuados na resolução das equações do 1º grau.
Depois desse entendimento podemos acelerar os processos de cálculo utilizando estratégias que simplificam e dão mais velocidade as contas.
Mas atenção! Jamais se esqueça do passo a passo realizado com o princípio aditivo pois isso é o que realmente acontece. Apenas otimizamos alguns passos já que isso é possível.
Então vamos lá!
Calculemos novamente a equação:
[math] x + 19 = 27 [/math]
O raciocínio que vamos adotar agora é simplesmente é isolar o termo que contém a variável em um lado da equação e deixar os termos sem a variável do outro.
[math] x = 27 - 19 [/math]
Dessa forma, adotamos o sinal de igual como o separador dos lados esquerdo e direito da equação. Ao providenciar este isolamento dos termos devemos adotar a seguinte regrinha: qualquer elemento que mudar de "lado" terá o seu sinal alterado. Simples assim.
O termo que tiver valor positivo passará a ter valor negativo e vice-versa. Somente o sinal é alterado.
Perceba que apenas o inteiro [math] + 19 [/math] "mudou" de lado e por isso agora ele se apresenta com o sinal negativo. Efetuando o cálculo do lado direito da equação obtemos:
[math] x = 8 [/math]
O mesmo resultado encontrado anteriormente quando aplicado o princípio aditivo. Na verdade ele continua ocorrendo, só omitimos aqueles cálculos para reduzir e acelerar as contas como mencionado. Compare e veja a economia de algumas linhas.
A ideia é essa. Ao utilizar este método prático, todo aquele processo de adicionar um termo é feito mentalmente. Com isso apenas a interpretação da resolução muda e seu resultado não. É como se um novo caminho fosse percorrido para chegar ao mesmo objetivo.
Vamos resolver o segundo exemplo agora para você entender a diferença.
[math] 2x + 8 = x - 3 [/math]
Começamos isolando os termos com variáveis de um lado e os sem variáveis do outro. Lembrando da troca de sinais para os termos que "mudarem de lado".

Apenas os termos [math] + 8 [/math] e [math] x [/math] vão trocar de lado aqui. Dessa forma teremos:
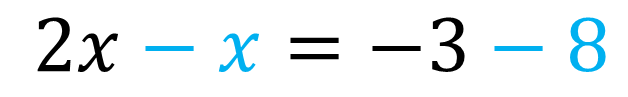
Efetuando os cálculos devidos em cada lado, finalmente chegamos ao resultado:
[math] x = - 11 [/math]
Exatamente o mesmo realizado pelo processo anterior. O ideal é que você caro aluno(a) resolva sempre utilizando as duas formas com a omissão ou não do princípio aditivo para ter um domínio cada vez maior deste assunto.
Que tal praticar um pouco?
“O importante é entender profundamente as coisas e as relações entre elas. É nisso que reside a inteligência.”
Laurent Schwartz
1) Encontre o valor da variável y para a equação [math] x + 4 = - 8 [/math]; sendo [math] U = \mathbb {R} [/math] (utilize o princípio aditivo).
2) Encontre o conjunto solução para a equação [math] 2x - 8 = x + 17 [/math]; sendo [math] U = \mathbb {Z} [/math] (utilize o princípio aditivo)
3) Encontre o valor da variável [math] y [/math] na equação [math] 2y + 119 = y - 220 [/math]; sendo [math] U = \mathbb {Z} [/math] (utilize o princípio aditivo)
4) O valor da incógnita na equação [math] x + 346 = 564 [/math]; sendo [math] U = \mathbb {R} [/math] é? (utilize o método prático)
5) Resolva a equação [math] 6b - 14 - 4b = 7b - 6b - 12 [/math] para [math] b \in \mathbb {R} [/math]. (utilize o método prático)

