Classificando ângulos
Em Geometria a classificação de objetos é muito comum. Isto facilita bastante na e identificação e memorização das características de cada um. Com os ângulos não será diferente. Veremos agora duas classificações muito importantes.
Classificação de ângulos quanto à amplitude
Os ângulos podem ser classificados de acordo com a sua amplitude (medida). Todos os ângulos abaixo, foram nomeados em função dela. Em alguns casos para facilitar, colocamos os lados dos ângulos com cores diferentes. Tenha como referência do ponto de partida sempre o lado direito do ângulo na horizontal.

ângulo nulo - ângulo com medida igual a 0°
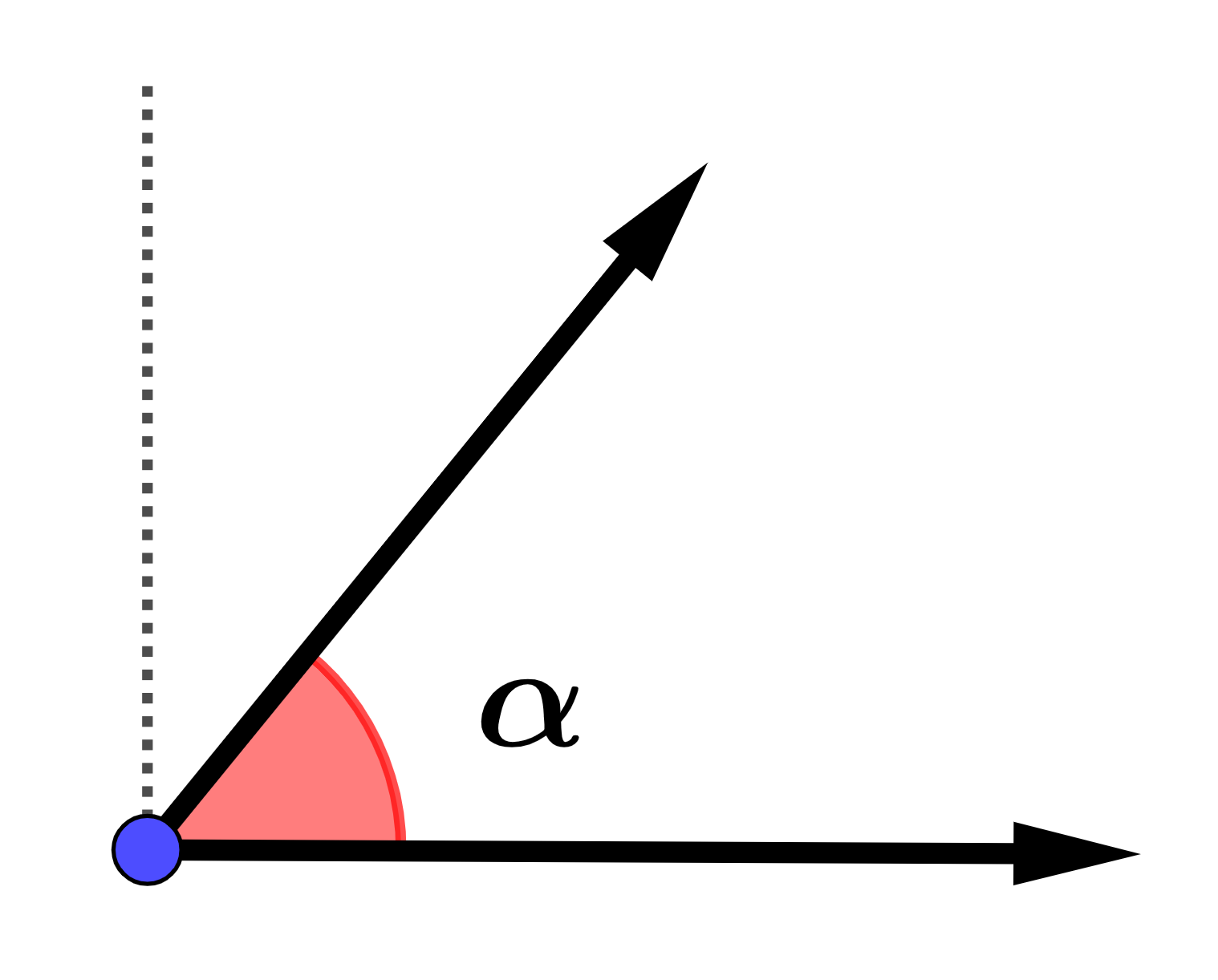
ângulo agudo - ângulo com medida menor que [math] 90° [/math]
[math] (0° < α < 90°) [/math]

ângulo reto - ângulo com medida igual a [math] 90° [/math]

ângulo obtuso - ângulo com medida maior que [math] 90° [/math]
[math] (90° < α < 180°) [/math]
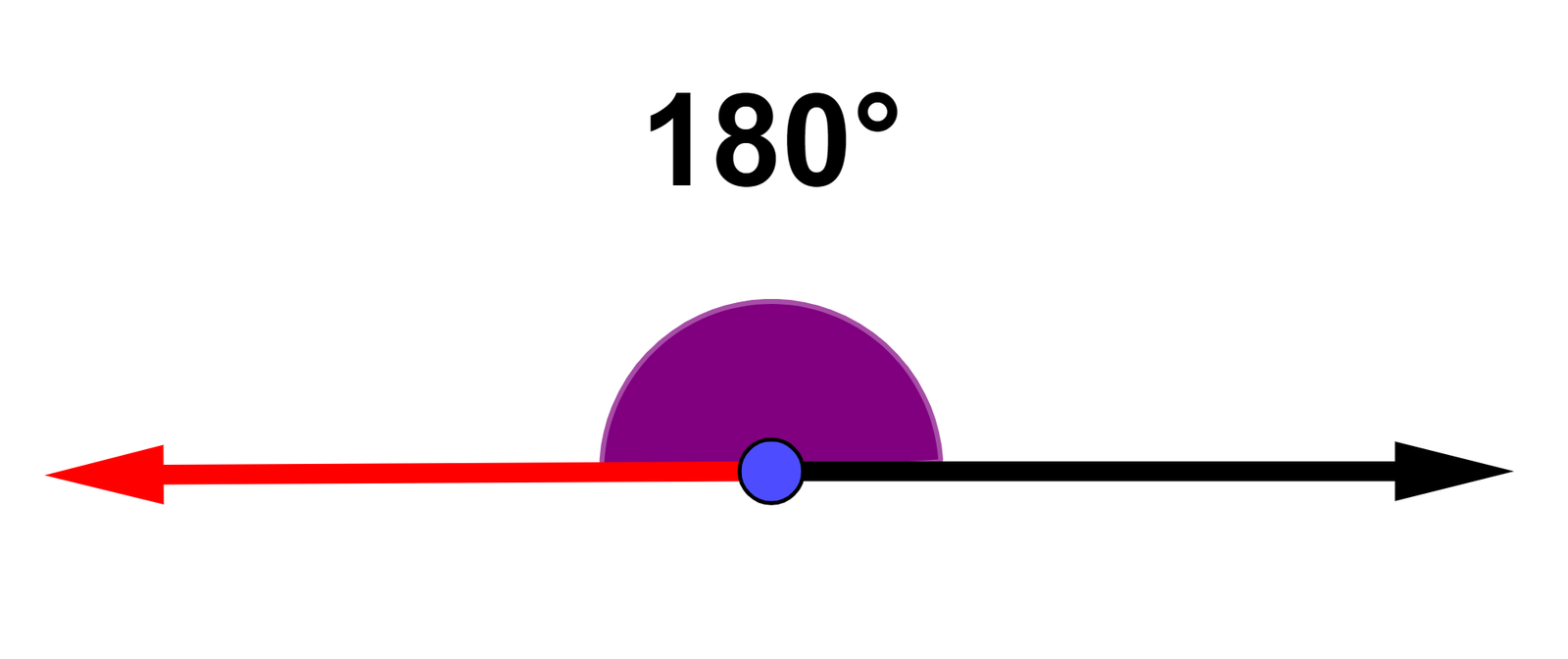
ângulo raso - ângulo com medida igual a [math] 180° [/math]
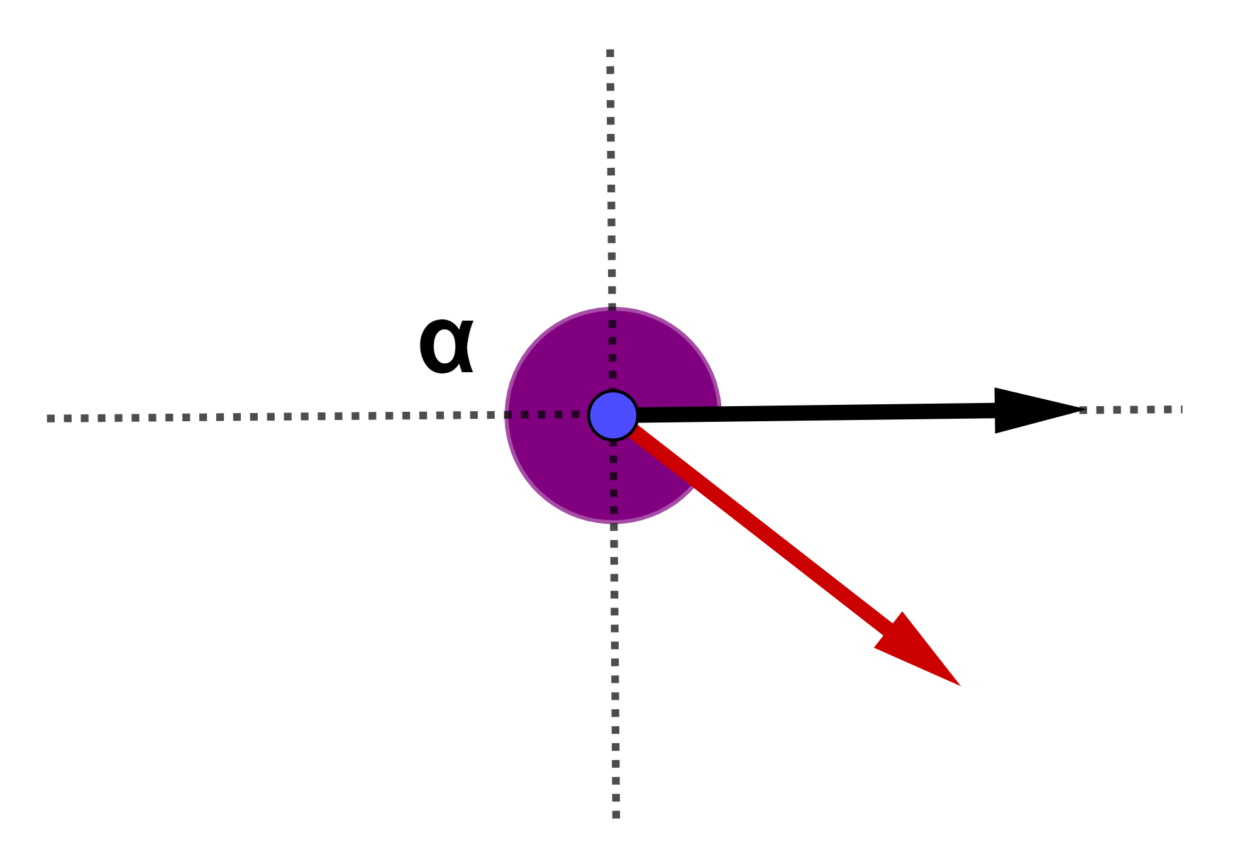
ângulo côncavo - ângulo com medida maior que [math] 180° [/math] e menor que [math] 360° [/math]
[math] (180° < α < 360°) [/math]

ângulo completo ou ângulo de uma volta -
ângulo com medida igual a [math] 360° [/math]
Classificação de ângulos quanto a sua posição
Para esta classificação, precisamos considerar sempre dois ou mais ângulos. Vamos conhecer cada uma delas.
Ângulos congruentes
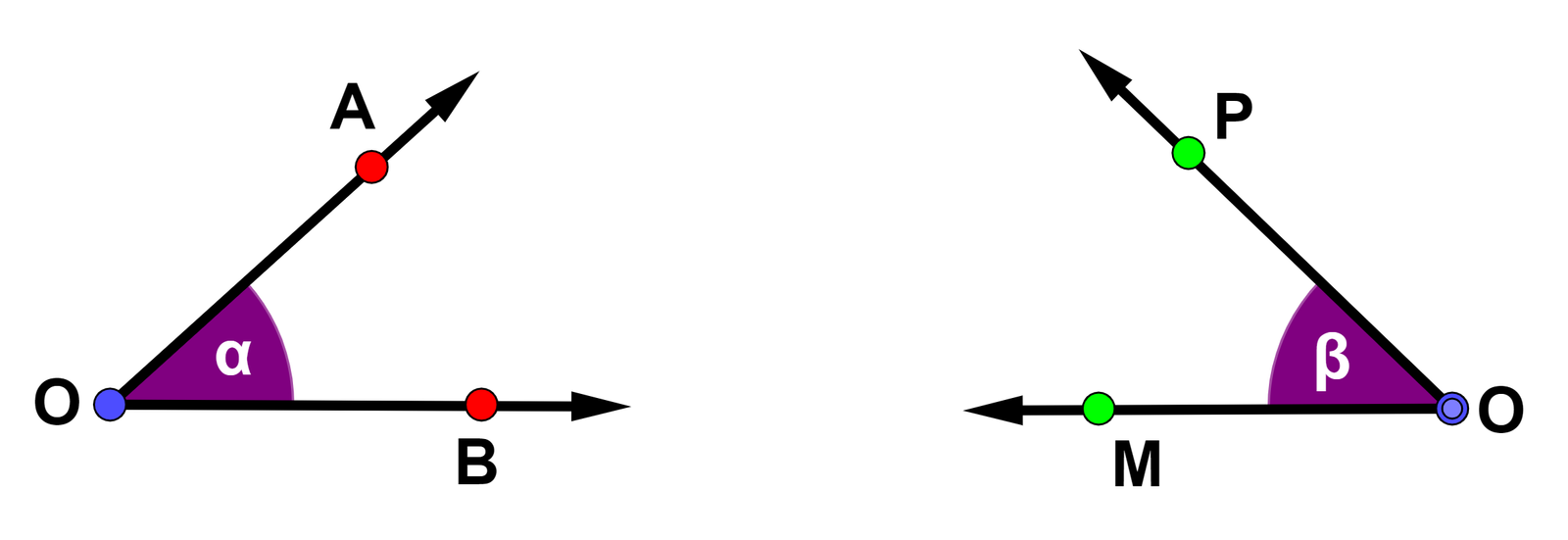
Dois ou mais ângulos são classificados como congruentes quando possuem a mesma medida (amplitude).
Na imagem acima temos um ângulo [math] m (A \widehat {O} B) = α [/math] e outro ângulo com [math] m (P \widehat {O} M) = β [/math]. Como vimos em ângulos, os símbolos significam respectivamente medida do ângulo [math] A \widehat {O} B [/math] igual a [math] α [/math] e medida do ângulo [math] P \widehat {O} M [/math] igual a [math] β [/math]. Sendo [math] α = β [/math], dizemos que os ângulos são congruentes (símbolo [math] \cong [/math]).
Dessa forma, já que [math] m (A \widehat {O} B) \cong m (P \widehat {O} M) [/math], então como consequência temos [math] A \widehat {O} P \cong P \widehat {O} M [/math]. Se as medidas dos ângulos são congruentes, então os ângulos também são.
Preste bem atenção pois os ângulos não são iguais e esta costuma ser uma confusão bastante comum. Eles possuem apenas a mesma medida como foi explicado. Se fossem iguais, os seus lados também teriam que ser iguais. Visível que os pontos nos lados dos ângulos são representados por letras diferentes.
Ângulos consecutivos
Dois ângulos são classificados como consecutivos quando possuem o mesmo vértice e um lado em comum.
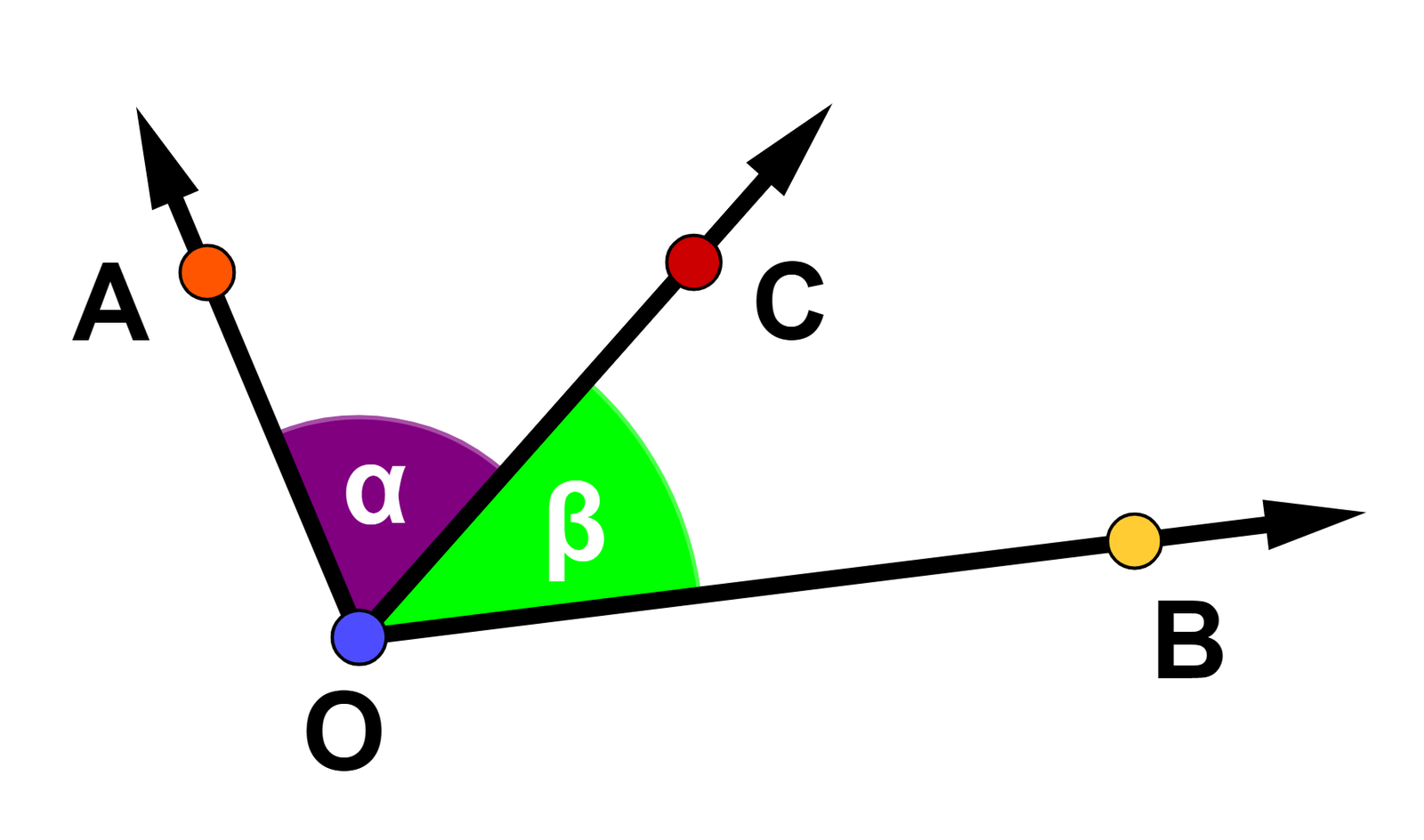
Como se pode ver, temos três ângulos na imagem: [math] A \widehat {O} C [/math], [math] C \widehat {O} B [/math] e [math] A \widehat {O} B [/math]. Vamos verificar se dois desses ângulos satisfazem as duas condições para que sejam classificados como consecutivos.
Vamos analisar os ângulos [math] A \widehat {O} C [/math] e [math] C \widehat {O} B [/math].
1) Possuem um vértice comum: [math] O [/math]
2) Possuem um lado comum: [math] \overline {\rm OC} [/math]
Como temos as duas condições satisfeitas, dizemos que os ângulos citados são consecutivos. Observe que sendo assim, não importa a posição dos ângulos. Basta que estas duas condições sejam satisfeitas para terem essa classificação.
Considere agora os ângulos [math] A \widehat {O} B [/math] e [math] C \widehat {O} B [/math]. Analisando obtemos:
1) Possuem vértice comum: [math] O [/math]
2) Possuem lado comum: [math] \overline {\rm {OB}} [/math]
Nesse caso os dois ângulos também são classificados como consecutivos.
Ângulos adjacentes
Dois ângulos são classificados como adjacentes quando não possuem pontos internos em comum.
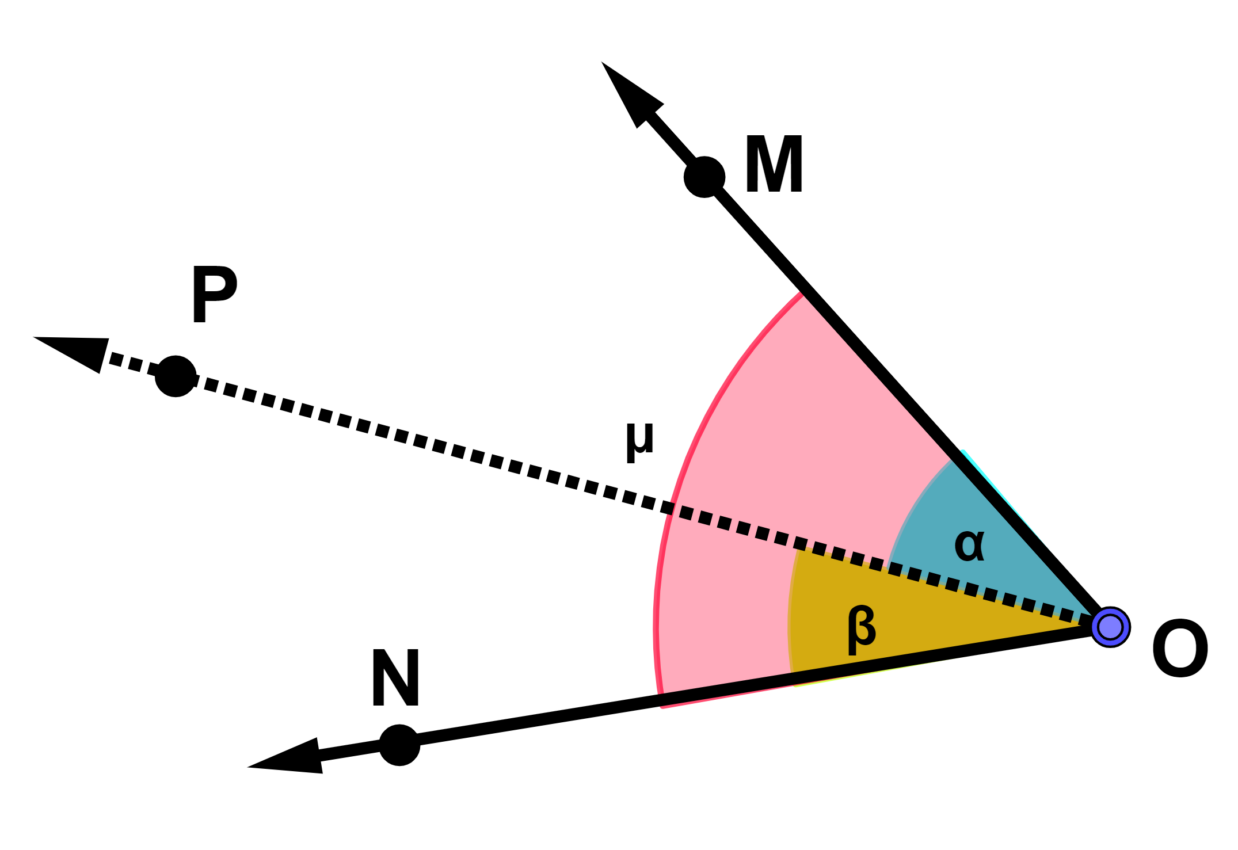
Na figura acima temos novamente três ângulos. Vamos primeiro considerar [math] P \widehat {O} M [/math] e [math] P \widehat {O} N [/math]. Analisando é possível notar que qualquer ponto inserido em uma região não se "mistura" com a outra. Dizemos que esses ângulos portanto, não possuem pontos internos em comum. Com essa condição classificamos esses dois ângulos como adjacentes.
Observe agora o ângulo [math] M \widehat {O} N [/math]. Alguns pontos desse ângulo também pertencem ao ângulo [math] P \widehat {O} M [/math]. O mesmo ocorre com o outro ângulo [math] P \widehat {O} N [/math]. Como ocorre essa "mistura" de alguns pontos dessas regiões, não poderíamos classificar nesse caso como adjacentes. Este é um exemplo clássico de ângulos que não possuem essa classificação.
Ângulos opostos pelo vértice (o.p.v.)

Dessa vez temos quatro ângulos na figura. As cores destacam os pares que vamos analisar. primeiro vamos considerar os pares de ângulos [math] A \widehat {O} B [/math] e [math] C \widehat {O} D [/math] destacados em verde. A única coisa comum aqui é o vértice e olhamos para a posição de ambos. Vamos considerar como se estivessem "frente a frente".
Quando nos deparamos com esses pares de ângulos, classificamos como opostos pelo vértice. Ângulos opostos pelo vértice serão sempre congruentes ([math] A \widehat {O} B \cong C \widehat {O} D [/math]).
Com o outro par de ângulos [math] A \widehat {O} C [/math] e [math] B \widehat {O} D [/math] destacados em azul ocorre o mesmo. Pela posição e o vértice em comum são também considerados opostos pelo vértice, portanto também congruentes ([math] A \widehat {O} C \cong B \widehat {O} D [/math]).
Observação: Retas concorrentes sempre vão formar dois pares de ângulos opostos pelo vértice, ou seja, dois pares de ângulos congruentes.
Vamos praticar?
"Coragem é saber o que não temer."
Platão
Continue praticando!
Gostaria de continuar praticando com mais exercícios como do questionário acima?
Se já for inscrito, faça login e procure pela página testes online para acesso imediato.
Agora caso ainda não seja cadastrado aqui no site, clique no botão logo abaixo, cadastre-se e tenha também acesso a algumas de nossas listas disponíveis.

